I seem to remember an EA forum post (or maybe on a personal blog) basically formalizing the idea (which is in Holden's original worldview diversification post) that with declining marginal returns and enough uncertainty, you will end up maximizing true returns with some diversification. (To be clear, I don't think this would apply much across many orders of magnitude.) However, I am struggling to find the post. Anyone remember what I might be thinking of?
Hide table of contents
Reactions
New Answer
New Comment
4 Answers sorted by
I was thinking about this recently too, and vaguely remember it being discussed somewhere and would appreciate a link myself.
To answer the question, here's a rationale for diversification that's illustrated in the picture below that I just whipped up.
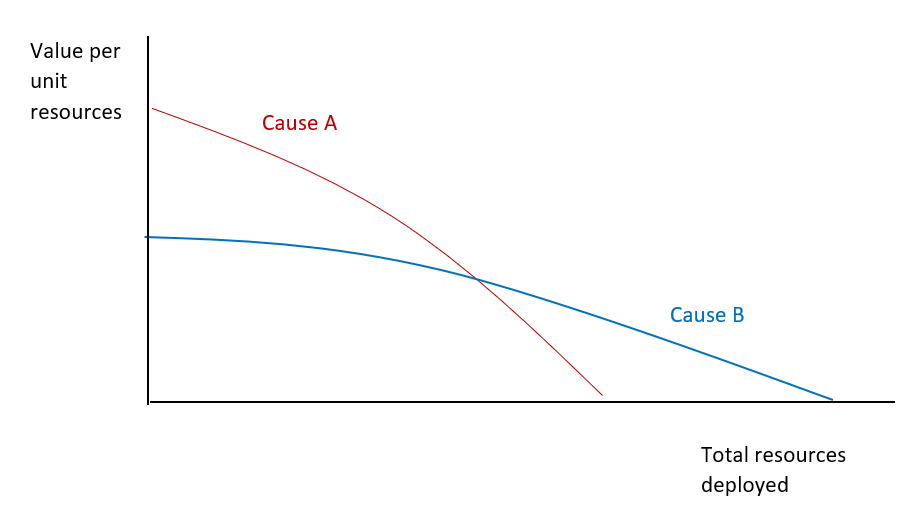
Imagine you have two causes where you believe their cost-effectiveness trajectories cross at some point. Cause A does more good per unit resources than cause B at the start but hits diminishing marginal returns faster than B. Suppose you have enough resources to get to the crossover point. What do you do? Well, you fund A up to that point, then switch to B. Hey presto, you're doing the most good by diversifying.
This scenario seems somewhat plausible in reality. Notice it's a justification for diversification that doesn't rely on appeals to uncertainty, either epistemic or moral. Adding empirical uncertainty doesn't change the picture: empirical uncertainty basically means you should draw fuzzy lines instead of precise ones, and it'll be less clear when you hit the crossover.
What's confusing for me about the worldview diversification post is that it seems to run together two justifications for, in practice, diversifying (i.e. supporting more than one thing) that are very different in nature.
One justification for diversification is based on this view about 'crossovers' illustrated above: basically, Open Phil has so much money, they can fund stuff in one area to the point of crossover, then start funding something else. Here, you diversify because you can compare different causes in common units and you so happen to hit crossovers. Call this "single worldview diversification" (SWD).
The other seems to rely on the idea there are different "worldviews" (some combination of beliefs about morality and the facts) which are, in some important way, incommensurable: you can't stick things into the same units. You might think Utilitarianism and Kantianism are incommensurable in this way: they just don't talk in the same ethical terms. Apples 'n' oranges. In the EA case, one might think the "worldviews" needed to e.g. compare the near-term to the long-term are, in some relevant sense incommensurable - I won't to try to explain that here, but may have a stab at in another post. Here, you might think you can't (sensibly) compare different causes in common units. What should you do? Well, maybe you give each of them some of your total resources, rather than giving it all to one. How much do you give each? This is a bit fishy, but one might do it on the basis of how likely you think each cause is really the best (leaving aside the awkward fact you've already said you don't think you can compare tem). So if you're totally unsure, each gets 50%. Call this "multiple worldview diversification" (MWD).*
Spot the difference: the first justification for diversification comes because you can compare causes, the second because you can't. I'm not sure if anyone has pointed this out before.
*I think MWD is best understood as an approach dealing with moral and/or empirical uncertainty. Depending on the type of uncertainty at hand, there are extant responses about how to deal with the problem that I won't go into here. One quick example: for moral uncertainty, you might opt for 'my favourite theory' and give everything to the theory in which you have most credence; see Bykvist (2017) for a good summary article on moral uncertainty.
I have two related posts, but they're about deep/model uncertainty/ambiguity, not precisely quantified uncertainty:
It sounds closer to the first one.
For precisely quantified distributions of returns, and expected return functions which depend only on how much is allocated to their corresponding project (and not to other projects), you can just use the expected return functions and forget about the uncertainty, and I think the following is very likely to be true (using appropriate distance metrics):
(Terminology: "weakly concave" means at most constant marginal returns, but possibly sometimes decreasing marginal returns; "strictly concave" means strictly decreasing marginal returns.)
If the expected value...
You might be thinking of this GPI paper:
given sufficient background uncertainty about the choiceworthiness of one’s options, many expectation-maximizing gambles that do not stochastically dominate their alternatives ‘in a vacuum’ become stochastically dominant in virtue of that background uncertainty
It has the point that with sufficient background uncertainty, you will end up maximizing expectation (i.e., you will maximize EV if you take stochastically dominated actions). But it doesn't have the point that you would add worldview diversification, though.
I don't remember a post but Daniel Kokotajlo recently said the following in a conversation. Someone with maths background should have an easy time to check & make this precise.
> It is a theorem, I think, that if you are allocating resources between various projects that each have logarithmic returns to resources, and you are uncertain about how valuable the various projects are but expect that most of your total impact will come from whichever project turns out to be best (i.e. the distribution of impact is heavy-tailed) then you should, as a first approximation, allocate your resources in proportion to your credence that a project will be the best.
This looks interesting, but I'd want to see a formal statement.
Is it the expected value that's logarithmic, or expected value conditional on nonzero (or sufficiently high) value?
tl;dr: I think under one reasonable interpretation, with logarithmic expected value and precise distributions, the theorem is false. It might be true if made precise in a different way.
If
- you only care about expected value,
- you had the expected value of each project as a function of resources spent (assuming logarithmic expected returns already assumes a lot, but does leave a lot of
Curated and popular this week
·
The cause prioritization landscape in EA is changing. Prominent groups have shut down, others have been founded, and everyone’s trying to figure out how to prepare for AI. This is the third in a series of posts critically examining the state of cause prioritization and strategies for moving forward.
Executive Summary
* An increasingly common argument is that we should prioritize work in AI over work in other cause areas (e.g. farmed animal welfare, reducing nuclear risks) because the impending AI revolution undermines the value of working in those other areas.
* We consider three versions of the argument:
* Aligned superintelligent AI will solve many of the problems that we currently face in other cause areas.
* Misaligned AI will be so disastrous that none of the existing problems will matter because we’ll all be dead or worse.
* AI will be so disruptive that our current theories of change will all be obsolete, so the best thing to do is wait, build resources, and reformulate plans until after the AI revolution.
* We identify some key cruxes of these arguments, and present reasons to be skeptical of them. A more direct case needs to be made for these cruxes before we rely on them in making important cause prioritization decisions.
* Even on short timelines, the AI transition may be a protracted and patchy process, leaving many opportunities to act on longer timelines.
* Work in other cause areas will often make essential contributions to the AI transition going well.
* Projects that require cultural, social, and legal changes for success, and projects where opposing sides will both benefit from AI, will be more resistant to being solved by AI.
* Many of the reasons why AI might undermine projects in other cause areas (e.g. its unpredictable and destabilizing effects) would seem to undermine lots of work on AI as well.
* While an impending AI revolution should affect how we approach and prioritize non-AI (and AI) projects, doing this wisel
·
TLDR
When we look across all jobs globally, many of us in the EA community occupy positions that would rank in the 99.9th percentile or higher by our own preferences within jobs that we could plausibly get.[1] Whether you work at an EA-aligned organization, hold a high-impact role elsewhere, or have a well-compensated position which allows you to make significant high effectiveness donations, your job situation is likely extraordinarily fortunate and high impact by global standards. This career conversations week, it's worth reflecting on this and considering how we can make the most of these opportunities.
Intro
I think job choice is one of the great advantages of development. Before the industrial revolution, nearly everyone had to be a hunter-gatherer or a farmer, and they typically didn’t get a choice between those.
Now there is typically some choice in low income countries, and typically a lot of choice in high income countries. This already suggests that having a job in your preferred field puts you in a high percentile of job choice. But for many in the EA community, the situation is even more fortunate.
The Mathematics of Job Preference
If you work at an EA-aligned organization and that is your top preference, you occupy an extraordinarily rare position. There are perhaps a few thousand such positions globally, out of the world's several billion jobs. Simple division suggests this puts you in roughly the 99.9999th percentile of job preference.
Even if you don't work directly for an EA organization but have secured:
* A job allowing significant donations
* A position with direct positive impact aligned with your values
* Work that combines your skills, interests, and preferred location
You likely still occupy a position in the 99.9th percentile or higher of global job preference matching. Even without the impact perspective, if you are working in your preferred field and preferred country, that may put you in the 99.9th percentile of job preference
·
I am writing this to reflect on my experience interning with the Fish Welfare Initiative, and to provide my thoughts on why more students looking to build EA experience should do something similar.
Back in October, I cold-emailed the Fish Welfare Initiative (FWI) with my resume and a short cover letter expressing interest in an unpaid in-person internship in the summer of 2025. I figured I had a better chance of getting an internship by building my own door than competing with hundreds of others to squeeze through an existing door, and the opportunity to travel to India carried strong appeal. Haven, the Executive Director of FWI, set up a call with me that mostly consisted of him listing all the challenges of living in rural India — 110° F temperatures, electricity outages, lack of entertainment… When I didn’t seem deterred, he offered me an internship.
I stayed with FWI for one month. By rotating through the different teams, I completed a wide range of tasks:
* Made ~20 visits to fish farms
* Wrote a recommendation on next steps for FWI’s stunning project
* Conducted data analysis in Python on the efficacy of the Alliance for Responsible Aquaculture’s corrective actions
* Received training in water quality testing methods
* Created charts in Tableau for a webinar presentation
* Brainstormed and implemented office improvements
I wasn’t able to drive myself around in India, so I rode on the back of a coworker’s motorbike to commute. FWI provided me with my own bedroom in a company-owned flat. Sometimes Haven and I would cook together at the residence, talking for hours over a chopping board and our metal plates about war, family, or effective altruism. Other times I would eat at restaurants or street food booths with my Indian coworkers. Excluding flights, I spent less than $100 USD in total. I covered all costs, including international transportation, through the Summer in South Asia Fellowship, which provides funding for University of Michigan under
It might be helpful to draw a dashed horizontal line at the maximum value for B, since you would fund A at least until the intersection of th... (read more)
If the uncertainty is precisely quantified (no imprecise probabilities), and the expected returns of each option depends only on how much you fund that option (and not how much you fund others), then you can just use the expected value functions.