Digital Sentience

Creating “digital sentience” is a lot harder than it looks. Standard Qualia Research Institute arguments for why it is either difficult, intractable, or literally impossible to create complex, computationally meaningful, bound experiences out of a digital computer (more generally, a computer with a classical von Neumann architecture) include the following three core points:

1. Digital computation does not seem capable of solving the phenomenal binding or boundary problems.
2. Replicating input-output mappings can be done without replicating the internal causal structure of a system.
3. Even when you try to replicate the internal causal structure of a system deliberately, the behavior of reality at a deep enough level is not currently understood (aside from how it behaves in light of inputs-to-outputs).

Let’s elaborate briefly:

The Binding/Boundary Problem

1. A moment of experience contains many pieces of information. It also excludes a lot of information. Meaning that, a moment of experience contains a precise, non-zero, amount of information. For example, as you open your eyes, you may notice patches of blue and yellow populating your visual field. The very meaning of the blue patches is affected by the presence of the yellow patches (indeed, they are “blue patches in a visual field with yellow patches too”) and thus you need to take into account the experience as a whole to understand the meaning of all of its parts.
2. A very rough, intuitive, conception of the information content of an experience can be hinted at with Gregory Bateson’s (1972) “a difference that makes a difference”. If we define an empty visual field as containing zero information, it is possible to define an “information metric” from this zero state to every possible experience by counting the number of Just Noticeable Differences (JNDs) (Kingdom & Prins, 2016) needed to transform such empty visual field into an arbitrary one (note: since some JND are more difficult to specify than others, a more accurate metric should also take into account the information cost of specifying the change in addition to the size of the change that needs to be made). It is thus evident to see that one’s experience of looking at a natural landscape contains many pieces of information at once. If it didn’t, you would not be able to tell it apart from an experience of an empty visual field.
3. The fact that experiences contain many pieces of information at once needs to be reconciled with the mechanism that generates such experiences. How you achieve this unity of complex information starting from a given ontology with basic elements is what we call “the binding problem”. For example, if you believe that the universe is made of atoms and forces (now a disproven ontology), the binding problem will refer to how a collection of atoms comes together to form a unified moment of experience. Alternatively, if one’s ontology starts out fully unified (say, assuming the universe is made of physical fields), what we need to solve is how such a unity gets segmented out into individual experiences with precise information content, and thus we talk about the “boundary problem”.
4. Within the boundary problem, as Chris Percy and I argued in Don’t Forget About the Boundary Problem! (2023), the phenomenal (i.e. experiential) boundaries must satisfy stringent constraints to be viable. Namely, among other things, phenomenal boundaries must be:
   1. Hard Boundaries: we must avoid “fuzzy” boundaries where information is only “partially” part of an experience. This is simply the result of contemplating the transitivity of the property of belonging to a given experience. If a (token) sensation A is part of a visual field at the same time as a sensation B, and B is present at the same time as C, then A and C are also both part of the same experience. Fuzzy boundaries would break this transitivity, and thus make the concept of boundaries incoherent. As a reductio ad absurdum, this entails phenomenal boundaries must be hard.
   2. Causally significant (i.e. non-epiphenomenal): we can talk about aspects of our experience, and thus we can know they are part of a process that grants them causal power. More so, if structured states of consciousness did not have causal effects in some way isomorphic to their phenomenal structure, evolution would simply have no reason to recruit them for information processing. Albeit epiphenomenal states of consciousness are logically coherent, the situation would leave us with no reason to believe, one way or the other, that the structure of experience would vary in a way that mirrors its functional role. On the other hand, states of consciousness having causal effects directly related to their structure (the way they feel like) fits the empirical data. By what seems to be a highly overdetermined Occam’s Razor, we can infer that the structure of a state of consciousness is indeed causally significant for the organism.
   3. Frame-invariant: whether a system is conscious should not depend on one’s interpretation of it or the point of view from which one is observing it (see appendix for Johnson’s (2015) detailed description of frame invariance as a theoretical constraint within the context of philosophy of mind).
   4. Weakly emergent on the laws of physics: we want to avoid postulating either that there is a physics-violating “strong emergence” at some level of organization (“reality only has one level” - David Pearce) or that there is nothing peculiar happening at our scale. Bound, casually significant, experiences could be akin to superfluid helium. Namely, entailed by the laws of physics, but behaviorally distinct enough to play a useful evolutionary role.
5. Solving the binding/boundary problems does not seem feasible with a von Neumann architecture in our universe. The binding/boundary problem requires the “simultaneous” existence of many pieces of information at once, and this is challenging using a digital computer for many reasons:
   1. Hard boundaries are hard to come by: looking at the shuffling of electrons from one place to another in a digital computer does not suggest the presence of hard boundaries. What separates a transistor's base, collector, and emitter from its immediate surroundings? What’s the boundary between one pulse of electricity and the next? At best, we can identify functional “good enough” separations, but no true physics-based hard boundaries.
   2. Digital algorithms lack frame invariance: how you interpret what a system is doing in terms of classic computations depends on your frame of reference and interpretative lens.
   3. The bound experiences must themselves be causally significant. While natural selection seemingly values complex bound experiences, our digital computer designs precisely aim to denoise the system as much as possible so that the global state of the computer does not influence in any way the lower-level operations. At the algorithmic level, the causal properties of a digital computer as a whole, by design, are never more than the strict sum of their parts.

Matching Input-Output-Mapping Does Not Entail Same Causal Structure

Even if you replicate the input-output mapping of a system, that does not mean you are replicating the internal causal structure of the system. If bound experiences are dependent on specific causal structures, they will not happen automatically without considerations for the nature of their substrate (which might have unique, substrate-specific, causal decompositions). Chalmers’ (1995) “principle of organizational invariance” assumes that replicating a system's functional organization at a fine enough grain will reproduce identical conscious experiences. However, this may be question-begging if bound experiences require holistic physical systems (e.g. quantum coherence). In such a case, the "components" of the system might be irreducible wholes, and breaking them down further would result in losing the underlying causal structure needed for bound experiences. This suggests that consciousness might emerge from physical processes that cannot be adequately captured by classical functional descriptions, regardless of their granularity.

More so, whether we realize it or not, it is always us (indeed complex bound experiences) who interpret the meaning of the input and the output of a physical system. It is not interpreted by the system itself. This is because the system has no real “points of view” from which to interpret what is going on. This is a subtle point, and will merely mention it for now, but a deep exposition of this line of argument can be found in The View From My Topological Pocket (2023).

We more so would point out that the system that is smuggling a “point of view” to interpret a digital computer’s operations is in the human who builds, maintains, and utilizes it. If we want a system to create its “own point of view” we will need to find the way for it to bind the information in a (1) “projector”/screen, (2) an actual point of view proper, or (3) the backwards lightcone that feeds into such a point of view. As argued, none of these are viable solutions.

Reality’s Deep Causal Structure is Poorly Understood

Finally, another key consideration that has been discussed extensively is that the very building blocks of reality have unclear, opaque causal structures. Arguably, if we want to replicate the internal causal structure of a conscious system, the classical input-output mapping is therefore not enough. If you want to ensure that what is happening inside the system has the same causal structure as its simulated counterpart, you would also need to replicate how the system would respond to non-standard inputs, including x-rays, magnetic fields, and specific molecules (e.g. Xenon isotopes).

These ideas have all been discussed at length in articles, podcasts, presentations, and videos. Now let’s move on to a more recent consideration we call “Costs of Embodiment”.

Costs of Embodiment

Classical “computational complexity theory” is often used as a silver bullet “analytic frame” to discount the computational power of systems. Here is a typical line of argument: under the assumption that consciousness isn’t the result of implementing a quantum algorithm per se, the argument goes, then there is “nothing that it can do that you couldn’t do with a simulation of the system”. This, however, is neglecting the complications that come from instantiating a system in the physical world with all that it entails. To see why, we must first explain the nature of this analytic style in more depth:

Introduction to Computational Complexity Theory

Computational complexity theory is a branch of computer science that focuses on classifying computational problems according to their inherent difficulty. It primarily deals with the resources required to solve problems, such as time (number of steps) and space (memory usage).

Key concepts in computational complexity theory include:

1. Big O notation: Used to describe the upper bound of an algorithm's rate of growth.
2. Complexity classes: Categories of problems with similar resource requirements (e.g., P, NP, PSPACE).
3. Time complexity: Measure of how the running time increases with the size of the input.
4. Space complexity: Measure of how memory usage increases with the size of the input.

In brief, this style of analysis is suited for analyzing the properties of algorithms that are implementation-agnostic, abstract, and interpretable in the form of pseudo-code. Alas, the moment you start to ground these concepts in the real physical constraints to which life is subjected, the relevance and completeness of the analysis starts to fall apart. Why? Because:

1. Big O notation counts how the number of steps (time complexity) or number of memory slots (space complexity) grows with the size of the input (or in some cases size of the output). But not all steps are created equal:
   1. Flipping the value of a bit might be vastly cheaper in the real world than moving the value of a bit to another location that is very (physically far) in the computer.
   2. Likewise, some memory operations are vastly more costly than others: in the real world you need to take into account the cost of redundancy, distributed error correction, and entropic decay of structures not in use at the time.
2. Not all inputs and outputs are created equal. Taking in some inputs might be vastly more costly than others (e.g. highly energetic vibrations that shake the system apart mean something to a biological organism as it needs to adapt to the possible stress induced by the nature of the input, expressing certain outputs might be much more costly than others, as the organism needs to reconfigure itself to deliver the result of the computation, a cost that isn’t considered by classical computational complexity theory).
3. Interacting with a biological system is a far more complex activity than interacting with, say, logic gates and digital memory slots. We are talking about a highly dynamic, noisy, soup of molecules with complex emergent effects. Defining an operation in this context, let alone its “cost”, is far from trivial.
4. Artificial computing architectures are designed, implemented, maintained, reproduced, and interpreted by humans who, if we are to believe already have powerful computational capabilities, are giving the system an unfair advantage over biological systems (which require zero human assistance).

Why Embodiment May Lead to Underestimating Costs

Here is a list of considerations that highlight the unique costs that come with real-world embodiment for information-processing systems beyond the realm of mere abstraction:

1. Physical constraints: Traditional complexity theory often doesn't account for physical limitations of real-world systems, such as heat dissipation, energy consumption, and quantum effects.
2. Parallel processing: Biological systems, including brains, operate with massive adaptive parallelism. This is challenging to replicate in classical computing architectures and may require different cost analyses.
3. Sensory integration: Embodied systems must process and integrate multiple sensory inputs simultaneously, which can be computationally expensive in ways not captured by standard complexity measures.
4. Real-time requirements: Embodied systems often need to respond in real-time to environmental stimuli, adding temporal constraints that may increase computational costs.
5. Adaptive learning: The ability to learn and adapt in real-time may incur additional computational costs not typically considered in classical complexity theory.
6. Robustness to noise: Physical systems must be robust to environmental noise and internal fluctuations, potentially requiring redundancy and error-correction mechanisms that increase computational costs.
7. Energy efficiency: Biological systems are often highly energy-efficient, which may come at the cost of increased complexity in information processing.
8. Non-von Neumann architectures: Biological neural networks operate on principles different from classical computers, potentially involving computational paradigms not well-described by traditional complexity theory.
9. Quantum effects: At the smallest scales, quantum mechanical effects may play a role in information processing, adding another layer of complexity not accounted for in classical theories.
10. Emergent properties: Complex systems may exhibit physical emergent properties that arise from the interactions of simpler components and as well as phase transitions, potentially leading to computational costs that are difficult to predict or quantify using standard methods.

See appendix for a concrete example of applying these considerations to an abstract and embodied object recognition system (example provided by Kristian Rönn).

Case Studies:

1.  2D Computers

It is well known in classical computing theory that a 2D computer can implement anything that an n-dimensional computer can do. Namely, because it is possible to create a 2D Turing Machine capable of simulating arbitrary computers of this class (to the extent that there is a computational complexity equivalence between an n-dimensional computer and a 2D computer), we see that (at the limit) the same runtime complexity as the original computer in 2D should be achievable.

However, living in a 2D plane comes with enormous challenges that highlight the cost of embodiment present in a given media. In particular, we will see that the *routing costs* of information will grow really fast, as the channels that connect between different parts of the computer will need to take turns in order to allow for the crossed wires to transmit information without saturating the medium of (wave/information) propagation.

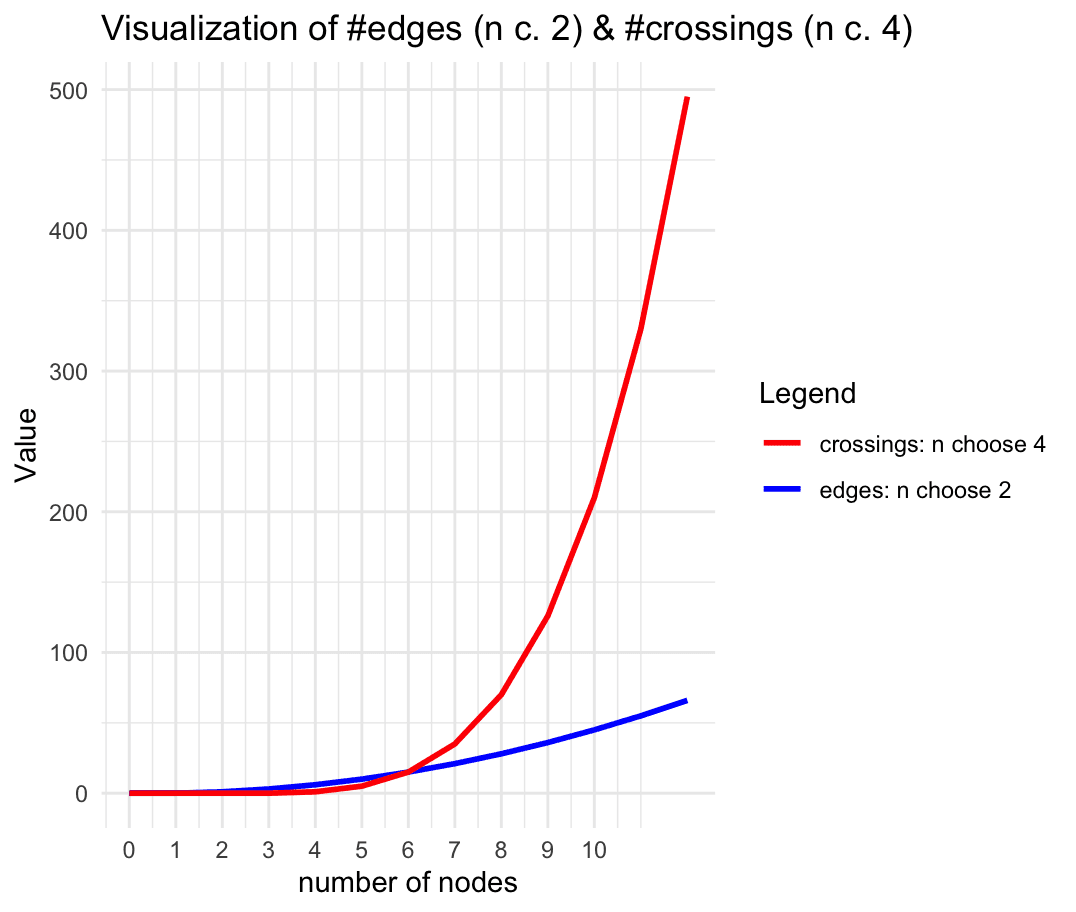
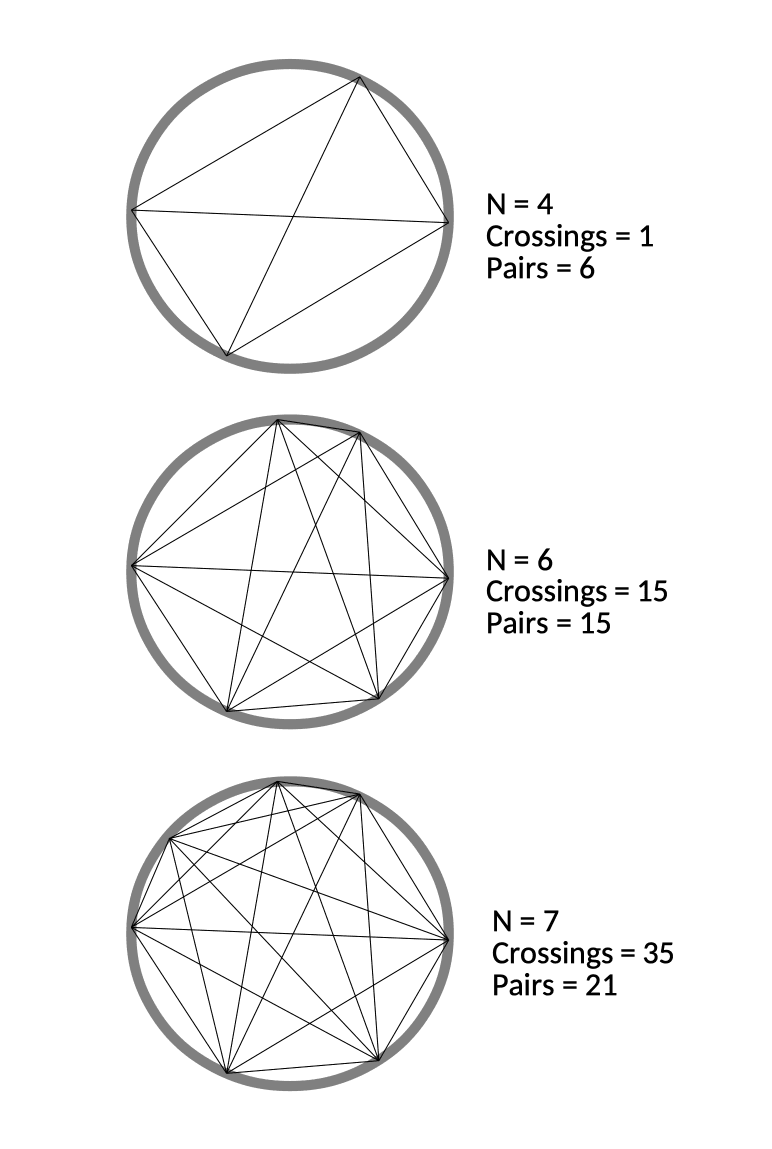
A concrete example here comes from examining what happens when you divide a circle into areas. Indeed, this is a well-known math problem, where you are supposed to derive a general formula for the number of areas by which a circle gets divided when you connect n (generally placed) points in its periphery. The takeaway of this exercise is often to point out that even though at first the number of areas seem to be powers of 2 (2, 4, 8, 16…) eventually the pattern is broken (the number after 16 is, surprisingly, 31 and not 32).

For the purpose of this example we shall simply focus on the growth of edges vs. the growth of crossings between the edges as we increase the number of nodes. Since every pair of nodes has an edge, the formula for the number of edges as a function of the number of nodes n is: n choose 2. Similarly, any four points define a single unique crossing, and thus the formula for the number of crossings is: n choose 4. When n is small (6 or less), the number of crossings is smaller or equal to the number of edges. But as soon as we hit 7 nodes, the number of crossings dominates over the number of edges. Asymptotically, in fact, the growth of edges is O(n^2) using the Big O notation, whereas the number of crossings ends up being O(n^4), which is much faster. If this system is used in the implementation of an algorithm that requires every pair of nodes to interact with each other once, we may at first be under the impression that the complexity will grow as O(n^2). But if this system is embodied, messages between the nodes will start to collide with each other at the crossings. Eventually, the number of delays and traffic jams caused by the embodiment of the system in 2D will dominate the time complexity of the system.

2. Blind Systems: Bootstrapping a Map Isn’t Easy

A striking challenge that biological systems need to tackle to instantiate moments of experience with useful information arises when we consider the fact that, at conception, biological systems lack a pre-existing "ground truth map" of their own components, i.e. where they are, and where they are supposed to be. In other words, biological systems somehow bootstrap their own internal maps and coordination mechanisms from a seemingly mapless state. This feat is remarkable given the extreme entropy and chaos at the microscopic level of our universe.

Assembly Theory (AT) (2023) provides an interesting perspective on this challenge. AT conceptualizes objects not as simple point particles, but as entities defined by their formation histories. It attempts to elucidate how complex, self-organizing systems can emerge and maintain structure in an entropic universe. However, AT also highlights the intricate causal relationships and historical contingencies underlying such systems, suggesting that the task of self-mapping is far from trivial.

Consider the questions this raises: How does a cell know its location within a larger organism? How do cellular assemblies coordinate their components without a pre-existing map? How are messages created and routed without a predefined addressing system and without colliding with each other? In the context of artificial systems, how could a computer bootstrap its own understanding of its architecture and component locations without human eyes and hands to see and place the components in their right place?

These questions point to the immense challenge faced by any system attempting to develop self-models or internal mappings from scratch. The solutions found in biological systems might potentially rely on complex, evolved mechanisms that are not easily replicated in classical computational architectures. This suggests that creating truly self-understanding artificial systems capable of surviving in a hostile, natural environment, may require radically different approaches than those currently employed in standard computing paradigms.

How Does the QRI Model Overcome the Costs of Embodiment?

This core QRI article presents a perspective on consciousness and the binding problem that aligns well with our discussion of embodiment and computational costs. It proposes that moments of experience correspond to topological pockets in the fields of physics, particularly the electromagnetic field. This view offers several important insights:

1. Frame-invariance: The topology of vector fields is Lorentz invariant, meaning it doesn't change under relativistic transformations. This addresses the need for a frame-invariant basis for consciousness, which we identified as a challenge for traditional computational approaches.
2. Causal significance: Topological features of fields have real, measurable causal effects, as exemplified by phenomena like magnetic reconnection in solar flares. This satisfies the requirement for consciousness to be causally efficacious and not epiphenomenal.
3. Natural boundaries: Topological pockets provide objective, causally significant boundaries that "carve nature at its joints." This contrasts with the difficulty of defining clear system boundaries in classical computational models.
4. Temporal depth: The approach acknowledges that experiences have a temporal dimension, potentially lasting for tens of milliseconds. This aligns with our understanding of neural oscillations and provides a natural way to integrate time into the model of consciousness.
5. Embodiment costs: The topological approach inherently captures many of the "costs of embodiment" we discussed earlier. The physical constraints, parallel processing, sensory integration, and real-time requirements of embodied systems are naturally represented in the complex topological structures of the brain's electromagnetic field.

This perspective suggests that the computational costs of consciousness may be even more significant than traditional complexity theory would indicate. It implies that creating artificial consciousness would require not just simulating neural activity, but replicating the precise topological structures of electromagnetic fields in the brain. This is a far more challenging task than conventional AI approaches.

Moreover, this view provides a potential explanation for why embodied systems like biological brains are so effective at producing consciousness. The physical structure of the brain, with its complex networks of neurons and electromagnetic fields, may be ideally suited to creating the topological pockets that correspond to conscious experiences. This suggests that embodiment is not just a constraint on consciousness, but a fundamental enabler of it.

Furthermore, there is a non-trivial connection between topological segmentation and resonant modes. The larger a topological pocket is, the lower the frequency of the resonant modes can be. This, effectively, is broadcasted to every region within the pocket (much akin how any spot on the surface of an acoustic guitar expresses the vibrations of the guitar as a whole). Thus, topological segmentation, quite conceivably, might be implicated in the generation of maps for the organism to self-organize around (cf. bioelectric morphogenesis according to Michael Levin, 2022). Steven Lehar (1999) and Michael E. Johnson (2018) in particular have developed really interesting conceptual frameworks for how harmonic resonance might be implicated in the computational character of our experience. The QRI insight that topology can mediate resonance, further complicates the role of phenomenal boundaries in the computational role of consciousness.

Conclusion and Path Forward

In conclusion, the costs of embodiment present significant challenges to creating digital sentience that traditional computational complexity theory fails to fully capture. The QRI solution to the boundary problem, with its focus on topological pockets in electromagnetic fields, offers a promising framework for understanding consciousness that inherently addresses many of these embodiment costs. Moving forward, research should focus on: (1) developing more precise methods to measure and quantify the costs of embodiment in biological systems, (2) exploring how topological features of electromagnetic fields could be replicated or simulated in artificial systems, and (3) investigating the potential for hybrid systems that leverage the natural advantages of biological embodiment while incorporating artificial components (cf. Xenobots). By pursuing these avenues, we may unlock new pathways towards creating genuine artificial consciousness while deepening our understanding of natural consciousness.

It is worth noting that the QRI mission is to “understand consciousness for the benefit of all sentient beings”. Thus, figuring out the constraints that give rise to computationally non-trivial bound experiences is one key piece of the puzzle: we don’t want to accidentally create systems that are conscious and suffering and become civilizationally load-bearing (e.g. organoids animated by pain or fear).

In other words, understanding how to produce conscious systems is not enough. We need to figure out how to (a) ensure that they are animated by information-sensitive gradients of bliss, and (b) how being empowered by the computational properties of consciousness can lean into more benevolent mind architectures. Namely, architectures that care about their wellbeing and the wellbeing of all sentient beings. This is an enormous challenge; clarifying the costs of embodiment is one key step forward, but part of an ecosystem of actions and projects needed for the robust positive impact of consciousness research for the wellbeing of all sentient beings.

Acknowledgments:

This post was written at the July 2024 Qualia Research Institute Strategy Summit in Sweden. It comes about as a response to incisive questions by Kristian Rönn on QRI’s model of digital sentience. Many thanks to Curran Janssen, Oliver Edholm, David Pearce, Alfredo Parra, Asher Soryl, Rasmus Soldberg, Erik Karlson, for brainstorming, feedback, suggesting edits, and the facilitation of this retreat.

Appendix

Excerpt from Michael E. Johnson’s Principia Qualia (2015) on Frame Invariance (pg. 61)

What is frame invariance?

A theory is frame-invariant if it doesn’t depend on any specific physical frame of reference, or subjective interpretations to be true. Modern physics is frame-invariant in this way: the Earth’s mass objectively exerts gravitational attraction on us regardless of how we choose to interpret it. Something like economic theory, on the other hand, is not frame-invariant: we must interpret how to apply terms such as “GDP” or “international aid” to reality, and there’s always an element of subjective judgement in this interpretation, upon which observers can disagree.

Why is frame invariance important in theories of mind?

Because consciousness seems frame-invariant. Your being conscious doesn’t depend on my beliefs about consciousness, physical frame of reference, or interpretation of the situation – if you are conscious, you are conscious regardless of these things. If I do something that hurts you, it hurts you regardless of my belief of whether I’m causing pain. Likewise, an octopus either is highly conscious, or isn’t, regardless of my beliefs about it.[a] This implies that any ontology that has a chance of accurately describing consciousness must be frame-invariant, similar to how the formalisms of modern physics are frame-invariant.

In contrast, the way we map computations to physical systems seems inherently frame-dependent. To take a rather extreme example, if I shake a bag of popcorn, perhaps the motion of the popcorn’s molecules could – under a certain interpretation – be mapped to computations which parallel those of a whole-brain emulation that’s feeling pain. So am I computing anything by shaking that bag of popcorn? Who knows. Am I creating pain by shaking that bag of popcorn? Doubtful... but since there seems to be an unavoidable element of subjective judgment as to what constitutes information, and what constitutes computation, in actual physical systems, it doesn’t seem like computationalism can rule out this possibility. Given this, computationalism is frame-dependent in the sense that there doesn’t seem to be any objective fact of the matter derivable for what any given system is computing, even in principle.

[a] However, we should be a little bit careful with the notion of ‘objective existence’ here if we wish to broaden our statement to include quantum-scale phenomena where choice of observer matters.

Example of Cost of Embodiment by Kristian Rönn

Abstract Scenario (Computational Complexity):

Consider a digital computer system tasked with object recognition in a static environment. The algorithm processes an image to identify objects, classifies them, and outputs the results.

Key Points:

• The computational complexity is defined by the algorithm's time and space complexity (e.g., O(n^2) for time, O(n) for space).
• Inputs (image data) and outputs (object labels) are well-defined and static.
• The system operates in a controlled environment with no physical constraints like heat dissipation or energy consumption.

However, this abstract analysis is extremely optimistic, since it doesn’t take the cost of embodiment into account.

Embodied Scenario (Embodied Complexity):

Now, consider a robotic system equipped with a camera, tasked with real-time object recognition and interaction in a dynamic environment.

Key Points and Costs:

1. Real-Time Processing:
   • The robot must process images in real-time, requiring rapid data acquisition and processing, which creates practical constraints.
   • Delays in computation can lead to physical consequences, such as collisions or missed interactions.
2. Energy Consumption:
   • The robot's computational tasks consume power, affecting the overall energy budget.
   • Energy management becomes crucial, balancing between processing power and battery life.
3. Heat Dissipation:
   • High computational loads generate heat, necessitating cooling mechanisms, requiring additional energy. Moreover, this creates additional costs/waste in the embodied system.
   • Overheating can degrade performance and damage components, requiring thermal management strategies.
4. Physical Constraints and Mobility:
   • The robot must move and navigate through physical space, encountering obstacles and varying terrains.
   • Computational tasks must be synchronized with motion planning and control systems, adding complexity.
5. Sensory Integration:
   • The robot integrates data from multiple sensors (camera, lidar, ultrasonic sensors) to understand its environment.
   • Processing multi-modal sensory data in real-time increases computational load and complexity.
6. Error Correction and Redundancy:
   • Physical systems are prone to noise and errors. The robot needs mechanisms for error detection and correction.
   • Redundant systems and fault-tolerance measures add to the computational overhead.
7. Adaptation and Learning:
   • The robot must adapt to new environments and learn from interactions, requiring active inference (i.e. we can’t train a new model everytime the ontology of an agent needs updating).
   • Continuous learning in an embodied system is resource-intensive compared to offline training in a digital system.
8. Physical Wear and Maintenance:
   • Physical components wear out over time, requiring maintenance and replacement.
   • Downtime for repairs affects the overall system performance and availability.

Pointers to Related Research

An Energy Complexity Model for Algorithms

Roy, S., Rudra, A., & Verma, A. (2013). https://doi.org/10.1145/2422436.2422470

Abstract

Energy consumption has emerged as a first class computing resource for both server systems and personal computing devices. The growing importance of energy has led to rethink in hardware design, hypervisors, operating systems and compilers. Algorithm design is still relatively untouched by the importance of energy and algorithmic complexity models do not capture the energy consumed by an algorithm. In this paper, we propose a new complexity model to account for the energy used by an algorithm. Based on an abstract memory model (which was inspired by the popular DDR3 memory model and is similar to the parallel disk I/O model of Vitter and Shriver), we present a simple energy model that is a (weighted) sum of the time complexity of the algorithm and the number of 'parallel' I/O accesses made by the algorithm. We derive this simple model from a more complicated model that better models the ground truth and present some experimental justification for our model. We believe that the simplicity (and applicability) of this energy model is the main contribution of the paper. We present some sufficient conditions on algorithm behavior that allows us to bound the energy complexity of the algorithm in terms of its time complexity (in the RAM model) and its I/O complexity (in the I/O model). As corollaries, we obtain energy optimal algorithms for sorting (and its special cases like permutation), matrix transpose and (sparse) matrix vector multiplication.

Thermodynamic Computing

Conte, T. et al. (2019). https://arxiv.org/abs/1911.01968

Abstract

The hardware and software foundations laid in the first half of the 20th Century enabled the computing technologies that have transformed the world, but these foundations are now under siege. The current computing paradigm, which is the foundation of much of the current standards of living that we now enjoy, faces fundamental limitations that are evident from several perspectives. In terms of hardware, devices have become so small that we are struggling to eliminate the effects of thermodynamic fluctuations, which are unavoidable at the nanometer scale. In terms of software, our ability to imagine and program effective computational abstractions and implementations are clearly challenged in complex domains. In terms of systems, currently five percent of the power generated in the US is used to run computing systems - this astonishing figure is neither ecologically sustainable nor economically scalable. Economically, the cost of building next-generation semiconductor fabrication plants has soared past $10 billion. All of these difficulties - device scaling, software complexity, adaptability, energy consumption, and fabrication economics - indicate that the current computing paradigm has matured and that continued improvements along this path will be limited. If technological progress is to continue and corresponding social and economic benefits are to continue to accrue, computing must become much more capable, energy efficient, and affordable. We propose that progress in computing can continue under a united, physically grounded, computational paradigm centered on thermodynamics. Herein we propose a research agenda to extend these thermodynamic foundations into complex, non-equilibrium, self-organizing systems and apply them holistically to future computing systems that will harness nature's innate computational capacity. We call this type of computing "Thermodynamic Computing" or TC.

Energy Complexity of Computation

Say, A.C.C. (2023). https://doi.org/10.1007/978-3-031-38100-3_1

Abstract

Computational complexity theory is the study of the fundamental resource requirements associated with the solutions of different problems. Time, space (memory) and randomness (number of coin tosses) are some of the resource types that have been examined both independently, and in terms of tradeoffs between each other, in this context. Since it is well known that each bit of information “forgotten” by a device is linked to an unavoidable increase in entropy and an associated energy cost, one can also view energy as a computational resource. Constant-memory machines that are only allowed to access their input strings in a single left-to-right pass provide a good framework for the study of energy complexity. There exists a natural hierarchy of regular languages based on energy complexity, with the class of reversible languages forming the lowest level. When the machines are allowed to make errors with small nonzero probability, some problems can be solved with lower energy cost. Tradeoffs between energy and other complexity measures can be studied in the framework of Turing machines or two-way finite automata, which can be rewritten to work reversibly if one increases their space and time usage.

Relevant physical limitations

• Landauer’s limit: The lower theoretical limit of energy consumption of computation.
• Bremermann's limit: A limit on the maximum rate of computation that can be achieved in a self-contained system in the material universe.
• Bekenstein bound: An upper limit on the thermodynamic entropy S, or Shannon entropy H, that can be contained within a given finite region of space which has a finite amount of energy.
• Margolus–Levitin theorem: A bound on the maximum computational speed per unit of energy.

References

Bateson, G. (1972). Steps to an ecology of mind. Chandler Publishing Company.

Chalmers, D. J. (1995). Absent qualia, fading qualia, dancing qualia. In T. Metzinger (Ed.), Conscious Experience. Imprint Academic. https://www.consc.net/papers/qualia.html

Gómez-Emilsson, A. (2023). The view from my topological pocket. Qualia Computing. https://qualiacomputing.com/2023/10/26/the-view-from-my-topological-pocket-an-introduction-to-field-topology-for-solving-the-boundary-problem/

Gómez-Emilsson, A., & Percy, C. (2023). Don’t forget the boundary problem! How EM field topology can address the overlooked cousin to the binding problem for consciousness. Frontiers in Human Neuroscience, 17. https://www.frontiersin.org/articles/10.3389/fnhum.2023.1233119 

Johnson, M. E. (2015). Principia qualia. Open Theory. https://opentheory.net/PrincipiaQualia.pdf

Johnson, M. E. (2018). A future of neuroscience. Open Theory. https://opentheory.net/2018/08/a-future-for-neuroscience/

Kingdom, F.A.A., & Prins, N. (2016). Psychophysics: A practical introduction. Elsevier.

Lehar, S. (1999). Harmonic resonance theory: An alternative to the "neuron doctrine" paradigm of neurocomputation to address gestalt properties of perception. http://slehar.com/wwwRel/webstuff/hr1/hr1.html

Levin, M. (2022). Bioelectric morphogenesis, cellular motivations, and false binaries with Michael Levin. DemystifySci Podcast. https://demystifysci.com/blog/2022/10/25/kl2d17sphsiw2trldsvkjvr91odjxv

Pearce, D. (2014). Social media unsorted postings. HEDWEB. https://www.hedweb.com/social-media/pre2014.html

Sharma, A. (2023). Assembly theory explains and quantifies selection and evolution. Nature, 622, 321–328. https://www.nature.com/articles/s41586-023-06600-9