There seems to be a widely-held view in popular culture that no physicist really understands quantum mechanics. The meme probably gained popularity after Richard Feynman famously stated in a lecture (transcribed in the book “The Character of Physical Law”) “I think I can safely say that nobody understands quantum mechanics”, though many prominent physicists have expressed a similar sentiment. Anyone aware of the overwhelming success of quantum mechanics will recognize that the seeming lack of understanding of the theory is primarily about how to interpret its ontology, and not about how to do the calculations or run the experiments, which clearly many physicists understand extremely well. But even the ontological confusion is debatable. With the proliferation of interpretations of quantum mechanics—each varying in terms of, among others, which classical intuitions should be abandoned—at least some physicists seem to think that there isn’t anything weird or mysterious about the quantum world.

So I suspect there are plenty of physicists who would politely disagree that it’s not possible to really understand quantum mechanics. Sure, it might take them a few decades of dedicated work in theoretical physics and a certain amount of philosophical sophistication, but there surely are physicists out there who (justifiably) feel like they grok quantum mechanics both technically and philosophically, and who feel deeply satisfied with the frameworks they’ve adopted. Carlo Rovelli (proponent of the relational interpretation) and Sean Carroll (proponent of the many-worlds interpretation) might be two such people.

This article is not about the controversial relationship between quantum mechanics and consciousness. Instead, I think there are some lessons to learn in terms of what it means and feels like to understand a difficult topic and to find satisfying explanations. Maybe you will relate to my own journey.

See, for a long time, I thought of consciousness as a fundamentally mysterious aspect of reality that we’d never really understand. How could we? Is there anything meaningful we can say about why consciousness exists, where it comes from, or what it’s made of? Well, it took me an embarrassingly long time to just read some books on philosophy of mind, but when I finally did some 10 years ago, I was captivated: What if we think in terms of the functions the brain carries out, like any other computing system? What if the hard problem is just ill-defined? Perhaps philosophical zombies can teach us meaningful things about the nature of consciousness? Wow. Maybe we can make progress on these questions after all! Functionalism in particular—the position that any information system is conscious if it computes the appropriate outputs given some inputs—seemed a particularly promising lens.

The floodgates of my curiosity were opened. I devoured as much content as I could on the topic—Dennett, Dehaene, Tononi, Russell, Pinker; I binge-read Brian Tomasik’s essays and scoured the EA Forum for any posts discussing consciousness. Maybe we can preserve our minds by uploading their causal structure? Wow, yes! Could sufficiently complex digital computers become conscious? Gosh, scary, but why not? Could video game characters matter morally? I shall follow the evidence wherever it leads me. The train to crazy town had departed, and I wanted to have a front-row seat.

Alas, the excitement soon started to dwindle. Somehow, the more I learned about consciousness, the more confused and dissatisfied I felt. Many times in the past I’d learned about a difficult topic (for instance, in physics, computer science, or mathematics) and, sure, the number of questions would multiply the more I learned, but I always felt like the premises and conclusions largely made sense and were satisfactory (even acknowledging the limitations of the field, such as classical mechanics). With consciousness, however, it was not that feeling. Could the US be conscious? Gee, I don’t know… If we ultimately care about functions/computations, which are inherently fuzzy, then maybe we can’t really quantify pleasure/suffering? Hmm. Or maybe consciousness is just an illusion that has to be “explained away”? Oof. (As the Buddhist joke goes, it’s all fun and games until somebody loses an ‘I’.)

So I kind of gave up around 2017 and largely stopped thinking about consciousness. To be clear, I think consciousness is very hard to understand. But my disillusionment came not from how hard the questions were, but by how unsatisfying the explanations felt. And yet these questions are obviously enormously important. Decisions about whether to fund work on, say, shrimp welfare or digital sentience, depend to a significant extent on getting these questions right. The same goes for decisions about which animals to eat (is passing the mirror test enough?), which beings the law should protect, whether to invest in “mind-uploading” technologies, etc.

About two years ago, however, my interest and enthusiasm for consciousness became reignited. Who would have guessed that I was not alone in finding functionalism unsatisfying and that alternative, scientifically rigorous theories existed? Suddenly, things started to click in a way that studying physics or mathematics clicked in the past. It didn’t take me long to finally give up on functionalism. And while I still have many questions about consciousness, for the first time I feel like the pieces of the puzzle are coming together, and that there’s a clear way forward.

My hope with this piece is to share a few intuition pumps that I have found helpful when thinking about consciousness in non-functionalist/computationalist terms. My goal is not to recreate the full, rigorous arguments against functionalism, but to plant some seeds of curiosity and give you a sense of the sorts of considerations that changed my mind. So let’s dive in.

Not all computers are computers

Consider the problem of computing the Fourier transform^[1] of a 2-dimensional image—say, an image of a white letter “A” on a black background:

The result is this other 2-dimensional image, representing the frequency spectrum of the original image:

OK, so how can we compute this Fourier transform? Here are three options:

Method 1: Run the Fast Fourier Transform algorithm on your digital computer: Simply feed the original image to your favorite implementation of the Fast Fourier Transform, e.g. in Python. Deep down, this will look like 0s and 1s being manipulated in smart ways by the computer’s processor in a deterministic way.

Method 2: Use a neural network that computes the Discrete Fourier Transform: It probably doesn’t make much sense to do it this way, but it’s possible.

Method 3: Build an optical setup with lenses and lasers: For example, by following these instructions. The setup will look as follows:

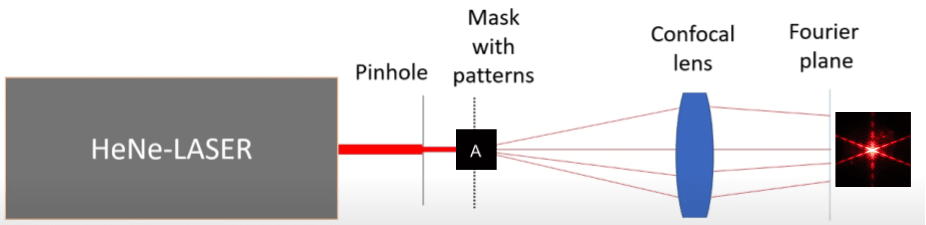
Basically, you shine a laser through a mask with the letter “A” and then have the beam pass through a lens. The Fourier transform will appear at some distance behind the lens.

As explained in the video, calculating the Fourier transform using method 1 with your average personal computer will take a couple of seconds, whereas the optical method takes ~0.3 nanoseconds (basically, the time it takes the light to travel from the mask plane to the Fourier plane). I know this is comparing apples to pears, but the point to take home is that you can exploit the physical properties of certain substrates (e.g., the electromagnetic properties of the laser and the crystalline structure and geometry of the lens) to perform some types of computations extremely efficiently.

How does the brain carry out computations? I used to think that the brain was basically a gigantic neural network. After all, artificial neural networks were heavily inspired by the neuron doctrine—the dominant paradigm in neuroscience—and we know that neural networks are universal function approximators. Clearly, neural networks play a key role in brain computation, but as neuroscientists start to question the neuron doctrine (e.g. given evidence of ephaptic coupling), a picture is starting to emerge where perhaps other processes more akin to method 3 could be taking place in the brain.

So far, I’ve only made the almost trivial observation that the properties of the substrate can matter for computation. What I have not (yet!) said is that they also matter for consciousness. However, I think it’s easy to get carried away by the seeming equivalence of brains and artificial neural networks and to therefore conclude that, whatever consciousness is, it should be captured at that level of abstraction. I certainly thought so for many years.

The problem of single-cell organisms

An additional hint pointing towards the inadequacy of neural networks to capture the full complexity of the brain is the fact that even single-cell organisms exhibit a wide array of seemingly complex behaviors. Single-cell organisms are thought to be capable of learning, integrating spatial information and adapting their behavior accordingly, deciding whether to approach or escape external signals, storing and processing information, and exhibiting predator-prey behaviors, among others. Attempts to use artificial neural networks have been shown to be “inefficient at modelling the single-celled ciliate’s avoidance reactions.” (Trinh, Wayland, Prabakara, 2019). “​​Given these facts, simple ‘summation-and-threshold’ models of neurons that treat cells as mere carriers of adjustable synapses vastly underestimate the processing power of single neurons, and thus of the brain itself.” (Tecumseh Fitch, 2021)

Again, here I’m simply pointing out that consciousness might not necessarily be something that emerges from sufficient neural network (connectionist) complexity, and that there might be other places to look.^[2]

Using “functionally equivalent” silicon neurons

One of the most common intuition pumps in favor of functionalist theories of consciousness is the idea that one can replace a carbon neuron with a silicon neuron as long as the silicon neuron faithfully reproduces the input/output mapping of the carbon neuron. But as we move away from a model of the neuron as a “summation-and-threshold” unit that simply receives (de)activation signals from the dendrites and generates output (de)activation signals through the axons, the task of creating functionally equivalent silicon neurons becomes more challenging. For instance, if it is in fact the electric fields generated by the neurons that allow the brain to represent and process information (cf. this MIT article), then the idea of using alternative silicon neurons starts to get complicated.

But is it possible? Well, consider again the optical setup that uses lasers and lenses to compute Fourier transforms, and focus on the lens, where arguably most of the computation takes place. What are the “functional units” performing the computations, analogous to the neurons in the brain? Is it the atoms in the lens? In what way can we replace parts of the lens with “functionally equivalent” parts made of some other arbitrary material? We could replace the whole lens with another “functionally equivalent” lens of a different optical material (say, borosilicate glass instead of fused silica), but certainly not with a lens of an arbitrary material.

To make this more precise, consider the fact that each point of the Fourier transform image is the result of nonlocal interference of light coming from all other points in the laser beam, as evidenced by the definition of the Fourier transform:

In other words, the intensity of the Fourier transform F at each point (x,y) is influenced by the laser intensity at other points, since we have to integrate over all points in 2D space. The upshot is that a local change (say, in a small region of the lens) can have effects everywhere on the resulting Fourier pattern. The notion of localized, functionally-replaceable units of computation breaks down when we consider these holistic forms of computation.

A skeptic might insist: Why not replace the whole lens with a functionally equivalent system composed of the following three elements:

1. A camera that receives the incoming laser beam with the letter “A”
2. A digital computer connected to the camera. This computer processes the digital image of the letter “A” and computes its Fourier transform (e.g. using the FFT algorithm)
3. A laser connected to the computer, which outputs a beam whose intensity is determined by the output of the FFT algorithm

Let’s ignore the fact that some resolution would get lost when the camera discretizes the incoming beam. While we could grant that the input and output of this new system are equivalent to the original lens, it would be way, way slower—the complexity of the FFT algorithm is O(n log n) whereas the lens always computes the Fourier transform at the speed of light, O(1). And this matters! To illustrate why, imagine now that you have a system of multiple lenses and lasers interacting with each other in intricate ways and in real time.^[3] Substituting any one lens with the three-part digital system would disrupt the whole setup because the computer is so much slower. So, no, from the perspective of the whole multi-lens setup, this replacement does not successfully preserve the functionality of the original lens.

To sum up, I believe it’s a mistake to assume that (a) neurons are the only computational units in the brain that matter, (b) neurons can be abstracted away as “summation-and-threshold” units, and (c) anything that reproduces the input/output of a neuron is a sufficiently good substitute for a neuron. Keep in mind the image of multiple lasers and lenses next time someone brings up this argument.^[4]

The binding problem

Look at this basketball:

What goes on in the brain as you look at the basketball? According to our best understanding of neuroscience, different parts of the brain carry out different subtasks, for example:

• The V1 area detects the black lines/edges as distinct from the orange background
• The V2 area responds to contrast in shading and lighting
• The V4 area processes its orange color
• The lateral occipital complex processes its round shape

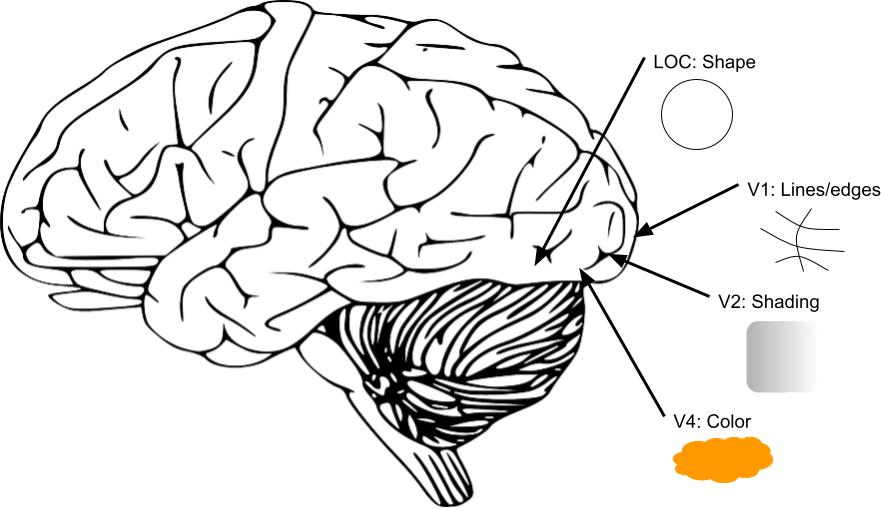
In reality, many parts of the brain can be involved in each subtask, so this breakdown is extremely simplified/wrong, but it’s sufficient for this argument.

Note that all of these different brain regions are spatially separated from each other. And yet, we consciously see a unified basketball with all its properties “glued”/bound together, even as it moves. How does the brain do this? This is the binding problem, and it remains an open question in neuroscience.

In addition, at any given moment, you can be conscious of multiple objects at a time (say, a basketball 🏀 and a player 🏃‍♀️), as well as of other sensory inputs (say, a bell ringing 🔔, the taste of popcorn in your mouth 👅, etc.). Similarly to the problem of binding the different features of the basketball into a unified object (local binding), your brain manages to bind all of these multiple sensory inputs into a coherent, unified landscape that makes up the entirety of your conscious experience at any given moment (global binding).

How many elements of our experience we can simultaneously pay attention to is a matter of debate, but that we can be consciously aware of multiple unified, cohesive entities simultaneously is as uncontroversial as the fact that you can perceive these two separate shapes at the same time: 🟩 🔵

It’s hard to overstate just how important binding is for human intelligence—indeed, for doing pretty much anything. It is at the core of how we process information and make sense of the world. Imagine not being able to bind together different features of objects into unified objects, or not being able to perceive more than one object at a time, or not being able to combine distinct events that occur at different times into a single, cohesive sequence of events (temporal binding). In fact, such conditions exist: Integrative agnosia, simultanagnosia, and akinetopsia, respectively. Needless to say, these conditions can be very debilitating. See this video of a woman with akinetopsia. Similarly, patients with ventral simultanagnosia are unable to read. Schizophrenia can be thought of as a malfunctioning of the binding that gives rise to a unitary self (Pearce, 2021).

To give you a sense of why this is such a difficult problem to solve if you assume that the brain is only a classical neural network, consider these two potential solutions:

1. “Conjunction” neurons: If some neuron fires when it sees a circle and another neuron fires when it sees something moving to the left, then perhaps there’s a third “circle moving to the left” neuron? Sadly, the number of such “conjunction” neurons would explode combinatorially, so this can’t be a solution. The same goes for suggesting that the two implicated neurons connect somehow (i.e., no third neuron) since the number of connections would also grow exponentially.

2. Neurons firing synchronously: Some have suggested it’s enough for the “circle” neuron and the “moving to the left” neuron to fire synchronously. But:

1. The two neurons are still spatially separated, so this doesn’t get to the root of the problem. (Plus: Which region of the brain is “noticing” or keeping track of the synchronicity? Wouldn’t that region also have a spatial extension?)
2. Neurons have been observed to fire synchronously in unconscious patients under anesthesia (Koch et al., 2016).
3. While neurons have been observed to fire synchronously during local binding (e.g. of shape and color), this is not always the case (Thiele and Stoner, 2003; Dong et al., 2008).
4. Special relativity tells us that synchronicity is relative and that no frame of reference is more correct than others. This implies that an observer traveling fast relative to you might conclude that your neurons are actually out of sync and that therefore you’re not experiencing a circle moving to the left, even though you say you are. Arguably, whether you are consciously experiencing a circle moving to the left or not shouldn’t be a matter of interpretation. (For example, if the traveling observer insisted she was right, but you kept earning points in a game that involved guessing which shapes move to which side, she’d be bewildered by your ability to do so.)^[5]

OK, so what does this all mean? Well, given that binding plays such a crucial role in human consciousness and intelligence, whatever theory of consciousness you think is correct better explain how binding happens. This applies regardless of whether you think binding does or doesn’t arise in artificial systems, or whether the qualia being bound are just illusions. I think it makes no sense to talk about consciousness without talking about binding.

I’ve yet to see a satisfactory functionalist account of how binding can happen (and I’ve come to believe that it’s not even possible in principle). At the same time, possible solutions positing that binding happens, for example, at the level of the electromagnetic fields produced by neurons strike me as elegant, parsimonious, and rigorous. This collection of papers with some of the most recent advances in the field is a good place to start for curious readers.^[6]

Most things are fuzzy, but not all things are fuzzy

Another very common intuition that proponents of functionalism or computationalism bring up is the observation that most things we typically think are real are actually fuzzy, and that we should have good reasons to believe that consciousness is actually also a fuzzy phenomenon. I recommend Tomasik (2017a, 2017b) and Muehlhauser (2017) for more details, but at the heart of this line of argument is the observation that whether we think something is, say, a table or not, is just a matter of interpretation. A big rock can be thought of as a table if people sit around it to have lunch. The same goes for more abstract concepts, such as “living organism”. We then notice that we seem puzzled about questions such as “Is a plant/bacterium/snail/etc. conscious?”. And so we (understandably) conclude that asking whether something is conscious or not might be closer to asking whether something is a table or not, than asking whether something is an electron or not.

Perhaps conveniently, computations/algorithms are also fuzzy. As Tomasik (2017b) explains, “a machine that implements the operation

0001, 0001 → 0010

could mean 1 + 1 = 2 (addition) but could also mean other possible functions, like 8, 8 → 4 if the binary digits are read from right to left, or 14, 14 → 13 if ‘0’ means what we ordinarily call ‘1’ and vice versa, and so on.” In other words, it’s really up to us as (arguably) conscious agents to interpret and decide what the operation 0001, 0001 → 0010 is supposed to mean—there’s no ultimate truth as to what the right interpretation is. Since there also doesn’t seem to be an ultimate truth as to what is conscious and what isn’t, we seem to have a match! So the question “Is X conscious?” is similar to asking “Does the computation above represent 1+1=2?”

I no longer believe this is how we should think about consciousness. I think the fuzziness intuition gets taken too far and causes people to give up too early on finding alternative explanations. So let’s restate the problem. What if we started from the assumption that consciousness is real (i.e., not fuzzy) in some meaningful sense, and then turned to existing physics and math to find structures that fit our ontological criteria?

Let me illustrate what I mean. All physicists would agree that tables are not ontological primitives, i.e., not really “real”. But is anything real? This is a much-debated question in the philosophy of science, but let’s take it step by step. First, consider that physicists work with a vast repertoire of quantities: mass, charge, energy, volume, length, electric field, weight, quark, etc. However, not all such quantities enjoy the same ontological status. A rock’s weight depends (by definition) on the gravitational force exerted on it. Similarly, a table’s length depends on how fast you’re moving relative to it when you measure it. So neither weight nor length are considered ontological primitives in physics. The spin of a field, on the other hand, does not depend on anything else—it just is what it is, no matter how you measure it (Berghofer, 2018). This makes some physicists think that spin—and, by extension, fields^[7]—are real and fundamental.

Is anything else real? For example, could certain configurations of those fields be considered real in some way? We know that fields can be configured such that they give rise to tables, rocks, remote controls, etc., all of which are fuzzy. But they can also be arranged to form, say, a hydrogen atom, which has properties that certainly do not depend on the observer. For example, the number of regions (“orbitals”) where the electron can be found is not a matter of interpretation, since orbitals are crisply, objectively divided by regions in space where the probability of finding the electron is exactly zero (the black lines/circles in the image below).

In short, if a certain physical property does not depend on the observer (i.e., it’s invariant), it is given special ontological status. For example, all quantities that are Lorentz invariant enjoy such status (Coffey, 2021^[8]; Benitez, 2023^[9]; François and Berghofer, 2024^[10]).

The upshot is: Maybe the question of whether a system (e.g., your best friend) is conscious or not should not depend on how you look at that system (the way looking at a rock from a certain angle makes it look like a table, or looking at an LLM from a certain angle makes it look conscious). If we commit to this (in my opinion, very reasonable) requirement, then the task is to identify consciousness with physical phenomena that, among other things, are invariant. The search is on, and promising candidates are being proposed, which makes it a very exciting time for consciousness research.

A note on emergence

You might be thinking “OK, let’s assume consciousness is some (Lorentz-invariant) physical phenomenon as opposed to a certain type of substrate-independent computation. That physical phenomenon is still just material, ‘dead’ stuff. Where does my phenomenal, first-person, subjective experience come from? I.e., how does this ontology solve the hard problem?” And you’d be justified in asking—we haven’t addressed this yet, and while I believe this is ultimately a question for philosophy, the physics-based ontology presented here can help us make sense of existing theories in philosophy of mind.

For example, consider that the (likely) strongest argument against panpsychism is the combination problem, namely, “how do the experiences of fundamental physical entities such as quarks and photons combine to yield the familiar sort of human conscious experience that we know and love.” (Chalmers, 2017) But once we realize that fundamental entities such as fields already give rise to all sorts of non-fuzzy, clearly delineated, observer-independent phenomena (from microscopic orbital clouds to macroscopic black holes), then we’re on to something. If you—like many physicists and philosophers^[11]—are willing to adopt the view that consciousness is fundamental (and perhaps exactly equivalent to the fields of physics, nothing more), then the combination problem of consciousness is no more mysterious than the “combination problem of black holes”. You then avoid the problem of strong emergence (Chalmers, 2006)^[12], since the properties of our consciousness would only be weakly emergent, in the same way that the properties of a black hole can be fully explained by the properties of its underlying components.

Functionalists typically (but not necessarily) struggle with the problem of strong emergence. How do certain types of computations give rise, at some level of complexity, to a completely new, ontological primitive (i.e., consciousness)? The most common answer is to deny that consciousness is actually an ontological primitive, e.g. it's rather an illusion. If you find this unsatisfying, consider talking to your doctor about panpsychism.

Parting thoughts

Tomasik (2017a) cites Dennett, the father of illusionism: “In Consciousness Explained, Dennett gives another example of a reduction that might feel unsatisfying (p. 454):

When we learn that the only difference between gold and silver is the number of subatomic particles in their atoms, we may feel cheated or angry—those physicists have explained something away: The goldness is gone from gold; they've left out the very silveriness of silver that we appreciate. [...] But of course there has to be some "leaving out"—otherwise we wouldn't have begun to explain. Leaving something out is not a feature of failed explanations, but of successful explanations.”

I agree that scientific theories don’t owe it to us to feel satisfying. But even with the ongoing debates around how to interpret quantum mechanics, or how to ultimately unify quantum mechanics with general relativity, by and large, our theories of physics happen to be extremely satisfying. Feynman’s famous quote is an apt response to Dennett. Perhaps we can expect our theories of consciousness to meet this bar?^[13]

1. ^{^}

   Here’s a nice, simplified explanation of the Fourier transform to refresh your memory if needed.

2. ^{^}

    I first heard this consideration from neuroscientist Justin Riddle here, who considers this to be a “glaring oversight in the neural network modeling domain”.

3. ^{^}

    In fact, optical computers are now being built.

4. ^{^}

    This consideration was inspired by a much more detailed and nuanced argument by Andrés Gómez Emilsson outlined in “Consciousness Isn't Substrate-Neutral: From Dancing Qualia & Epiphenomena to Topology & Accelerators”, video version.

5. ^{^}

    I first encountered this argument in “Solving the Phenomenal Binding Problem: Topological Segmentation as the Correct Explanation Space” by Andrés Gómez Emilsson.

6. ^{^}

    I’m grateful to David Pearce for emphasizing the importance of the binding problem, and to Andrés Gómez Emilsson for elucidating how electromagnetic field theories can solve the binding/boundary problem.

7. ^{^}

    There are 17 fundamental fields in the Standard Model of physics, which give rise to all the fundamental particles (electrons, photons, etc.) when they vibrate.

8. ^{^}

    Cf. Section 3: “Second, and relatedly, that any numerical quantities representing primitive or basic physical properties are Lorentz-invariant—that is, are not frame- or observer-dependent.”

9. ^{^}

    Cf. Section 5: “The basic argument is an extension to theoretical symmetries of an argument that goes back to Lange (2001), where it is argued that Lorentz invariance should be a requirement for ontological commitment in relativistic theories. The reasoning behind this is that what is real should not depend on arbitrary choices made by the observer.”

10. ^{^}

     Cf. Section 1: “[…] there is noticeable consensus among physicists that physically real quantities must be gauge-invariant.” For a technical account of the relationship between Lorentz invariance and gauge invariance, see e.g. Rivat 2023.

11. ^{^}

     Arguably, David Chalmers, Thomas Nagel, Bertrand Russell, David Bohm, etc.

12. ^{^}

     As David Pearce points out, strong emergence is not compatible with the laws of physics, and should therefore be avoided.

13. ^{^}

     Many ideas in this post have been presented in greater detail elsewhere, in particular in the writings of Andrés Gómez Emilsson (and others at Qualia Research Institute), David Pearce, and Mike Johnson. I might be misunderstanding, misrepresenting, or oversimplifying some of their ideas, so I recommend reading their content directly.