This post outlines some incentive problems with forecasting tournaments, such as Good Judgement Open, CSET, or Metaculus. These incentive problems may be problematic not only because unhinged actors might exploit them, but also because of mechanisms such as those outlined in Unconscious Economics. For a similar post about PredictIt, a prediction market in the US, see here. This post was written in collaboration with Nuño Sempere, who should be added as a coauthor soon. This is a crosspost from LessWrong.
Problems
Discrete prizes distort forecasts
If a forecasting tournament offers a prize to the top X forecasters, the objective "be in the top X forecasters" differs from "maximize predictive accuracy". The effects of this are greater the smaller the number of questions.
For example if only the top forecaster wins a prize, you might want to predict a surprising scenario, because if it happens you will reap the reward, whereas if the most likely scenario happens, everyone else will have predicted it too.
Consider for example this prediction contest, which only had a prize for #1. The following question asks about the margin Biden would win or lose Georgia by:
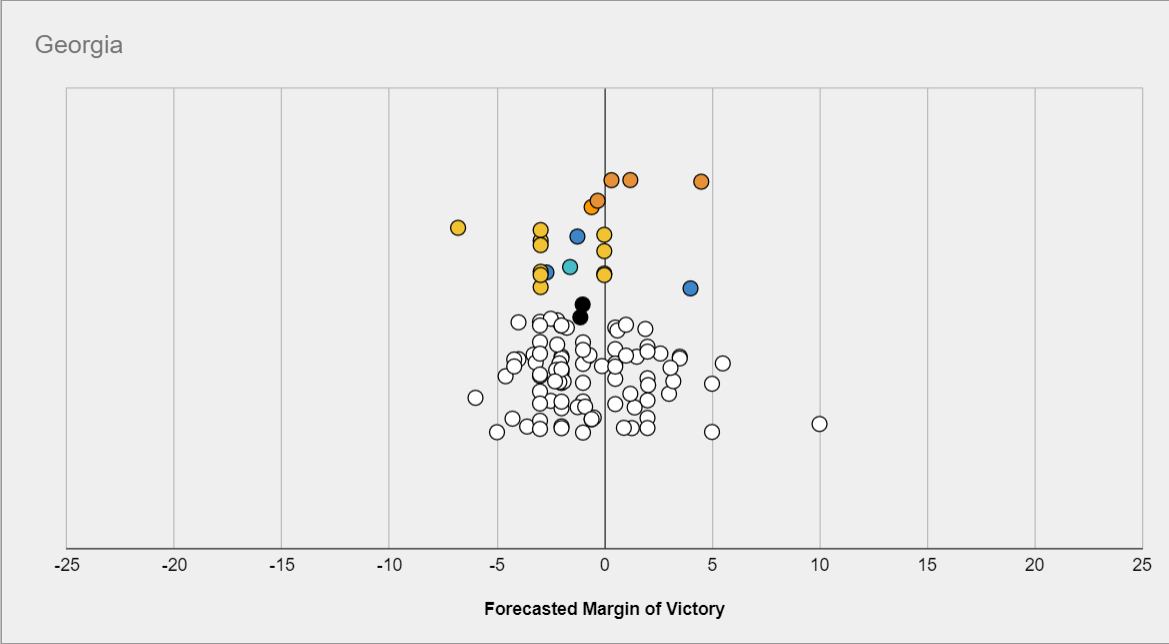
Then the most likely scenario might be a close race, but the prediction which would have maximized your odds of coming in #1st might be much more extremized, because other predictors are more tightly packed in the middle.
This effect also applies if you think of "becoming a superforecaster", which you can do if you are in the top 2% and have over 100 predictions in Good Judgement Open, as a distinct objective from "maximizing reward accuracy".
Incentives not to share information and to produce corrupt information
In a forecasting tournament, there is a disincentive to sharing information, because other forecasters can use it to improve relative standing. This not only includes not sharing information but also providing misleading information. As a counterpoint, other forecasters can and will often point out flaws in your reasoning if you're wrong.
Incentives to selectively pick questions.
If one is maximizing the Brier score, one is incentivized to pick easier questions. Specifically, if someone has a brier score b2, then they should not make a prediction on any question where the probability is between b and (1-b), even if they know the true probability exactly. Tetlock explicitly mentions this in one of his Commandments for superforecasters: “Focus on questions where your hard work is likely to pay off”. Yet if we care about making better predictions of things we need to know the answer to, the skill of "trying to answer easier questions so you score better" is not a skill we should reward, let alone encourage the development of.
A related issue is that, if one is maximizing the difference between one's Brier score and the aggregate’s Brier score, one is incentivized to pick questions for which the one thinks the aggregate is particularly wrong. This is not necessarily a problem, but can be.
Incentive to just copy the community on every question.
In scoring systems which more directly reward making many predictions, such as the Metaculus scoring system where in general one has to be both wrong and very confident to actually lose points, predictors are heavily incentivized to make predictions on as many questions as possible in order to move up the leaderboard. In particular, a strategy of “predict the community median with no thought” could see someone rise to the top 100 with a few months of signing up.
This is plausibly less bad than the incentives above, although this depends on your assumptions. If the main value of winning “metaculus points” is personal satisfaction, then predicting exactly the community median is unlikely to keep people entertained for long. New users predicting something fairly close to the community median on lots of questions, but updating a little bit based on their own thinking, is arguably not a problem at all, as the small adjustments may be enough to improve the crowd forecast, and the high volume of practice that users with this strategy experience can lead to rapid improvement.
Solutions
Probabilistic rewards
In tournaments with fairly small numbers of questions, where paying only the top few places would incentivize forecasters to make overconfident predictions to maximize their chance of first-place finishes as discussed above, probabilistic rewards may be used to mitigate this effect.
In this case, rather than e.g. having prizes for the top three scorers, prizes would be distributed according to a lottery, where the number of tickets each player received was some function of their score, thereby incentivizing players to maximize their expected score, rather than their chance of scoring highest.
Which precise function should be used is a non-trivial question: If the payout structure is too “flat”, then there is not sufficient incentive for people to work hard on their forecasts compared to just entering with the community median or some reasonable prior. If on the other hand the payout structure too heavily rewards finishing in one of the top few places, then the original problem returns. This seems like a promising avenue for a short research project or article.
Giving rewards to the best forecasters among many questions.
If one gives rewards to the top three forecasters for 10 questions in a contest in which there are 200 forecasters, the top three forecasters might be as much a function of luck as of skill, which might be perceived as unfair. Giving prizes for much larger pools of questions makes this effect smaller.
Forcing forecasters to forecast on all questions
This fixes the incentive to pick easier questions to forecast on.
A similar idea is assuming that forecasters have predicted the community median on any question that they haven't forecast on, until they make their own prediction, and then reporting the average brier score over all questions. This has the disadvantage of not rewarding "first movers/market makers", however it has the advantage of "punishing" people for not correcting a bad community median in a way that relative Brier doesn't (at least in terms of how people experience it).
Scoring groups
If one selects a group of forecasters and offers to reward them in proportion to the Brier score of the group’s predictions for a fixed set of questions, then the forecasters now have the incentive to share information with the group. This group of forecasters could be pre-selected for having made good predictions in the past.
Designing collaborative scoring rules
One could design rules around, e.g., Shapley values, but this is tricky to do. Currently, some platforms make it possible to give upvotes to the most insightful forecasters, but if upvotes were monetarily rewarded, one might not have the incentive to upvote other participants’ contributions as opposed to waiting for one’s contributions to be upvoted.
In practice, Metaculus and GJOpen do have healthy communities which collaborate, where trying to maximize accuracy at the expense of other forecasters is frowned upon, but this might change with time, and it might not always be replicable. In the specific case of Metaculus, monetary prizes are relatively new, but becoming more frequent. It remains to be seen whether this will change the community dynamic.
Divide information gatherers and prediction producers.
In this case, information gatherers might then be upvoted by prediction producers, who wouldn’t have any disincentive not to do so. Alternatively, some prediction producers might be shown information from different information gatherers, or select which information was responsible for a particular change in their forecast. A scheme in which the two tasks are separated might also lead to efficiency gains.
Other ideas
- One might explicitly reward reasoning rather than accuracy (this has been tried on Metaculus for the insight tournament, and also for the El Paso series). This has its own downsides, notably that it’s not obvious that reasoning which looks good/reads well is actually correct.
- One might make objectives more fuzzy, like the Metaculus points system, hoping this would make it more difficult to hack.
- One might reward activity, i.e., frequency of updates, or some other proxy expected to correlate with forecasting accuracy. This might work better if the correlation is causal (i.e., better forecasters have higher accuracy because they forecast more often), rather than due to a confounding factor. The obvious danger with any such strategy is that rewarding the proxy is likely to break the correlation.

This is great, and it deals with a few points I didn't, but here's my tweetstorm from the beginning of last year about the distortion of scoring rules alone:
https://twitter.com/davidmanheim/status/1080458380806893568
If you're interested in probability scoring rules, here's a somewhat technical and nit-picking tweetstorm about why proper scoring for predictions and supposedly "incentive compatible" scoring systems often aren't actually a good idea.
First, some background. Scoring rules are how we "score" predictions - decide how good they are. Proper scoring rules are ones where a predictor's score is maximized when it give it's true best guess. Wikipedia explains; en.wikipedia.org/wiki/Scoring_r…
A typical improper scoring rule is the "better side of even" rule, where every time your highest probability is assigned to the actual outcome, you get credit. In that case, people have no reason to report probabilities correctly - just pick a most likely outcome and say 100%.
There are many proper scoring rules. Examples include logarithmic scoring, where your score is the log of the probability assigned to the correct answer, and Brier score, which is the mean squared error. de Finetti et al. lays out the details here; link.springer.com/chapter/10.100…
These scoring rules are all fine as long as people's ONLY incentive is to get a good score.
In fact, in situations where we use quantitative rules, this is rarely the case. Simple scoring rules don't account for this problem. So what kind of misaligned incentives exist?
Bad places to use proper scoring rules #1 - In many forecasting applications, like tournaments, there is a prestige factor in doing well without a corresponding penalty for doing badly. In that case, proper scoring rules incentivise "risk taking" in predictions, not honesty.
Bad places to use proper scoring rules #2 - In machine learning, scoring rules are used for training models that make probabilistic predictions. If predictions are then used to make decisions that have asymmetric payoffs for different types of mistakes., it's misaligned.
Bad places to use proper scoring rules #3 - Any time you want the forecasters to have the option to say answer unknown. If this is important - and it usually is - proper scoring rules can disincentify or overincentify not guessing, depending on how that option is treated.
Using a metric that isn't aligned with incentives is bad. (If you want to hear more, follow me. I can't shut up about it.)
Carvalho discusses how proper scoring is misused; https://viterbi-web.usc.edu/~shaddin/cs699fa17/docs/Carvalho16.pdf
Anyways, this paper shows a bit of how to do better; https://pubsonline.informs.org/doi/abs/10.1287/deca.1110.0216
Fin.
I enjoyed this tweetstorm when you mentioned it to me and should have highlighted it in the article as useful further reading, thanks for posting it!
Hey all-
I'm one of the developers at Cultivate Labs, the company that builds the forecasting platform for GJOpen and CSET Foretell. Really enjoyed the post. I get the sense that some of you may already know a bunch of this, but thought it might be worth chiming in:
Re: Incentives to selectively pick questions.
In the scoring system we typically use (Relative Brier Scores aka Net Brier Points), this tends to not be an issue (as suggested in the last paragraph of that section). You're incentivized to forecast on questions where you think you can improve the aggregate forecast, which is exactly what we want.
By using a relative score, it also negates the need to force people to forecast on every question, since not forecasting gives you no score, which is effectively the median score. Copying the community forecast also becomes moot, since you get the same result by not forecasting. This system also does reward "first movers" since you can accumulate points each day -- forecasts that are early & accurate will get a better score than those that are late & accurate.
Re: Incentives not to share information and to produce corrupt information
I agree with this in relation to forecaster rationales. My incentive is to not share new nuggets of information I used to formulate my forecast. A saving grace here, though, is that my forecast is still plainly visible. I could write a rationale trying to mislead people in order to encourage bad forecasts from them, but I'm unable to hide it if I forecast contrary to my misleading rationale. You still know my true beliefs -- my probabilities.
Re: Discrete prizes distort forecasts
I agree that this is a challenge and it regularly concerns me that we're creating perverse incentives. We've used the probabilistic rewards approach in the past and it seemed somewhat helpful. Generally, I think avoiding a top-heavy reward system is important and helpful.
One quasi-related and interesting thing, though, is that research has shown that the aggregate forecast is often not extreme enough and that you can improve the brier of the crowd by directly extremizing the aggregate forecast.
One of the biggest/most frequent complaints that we hear about our current system is that a Brier penalize misses more than it rewards hits. You can see this in the Raw Score vs. Probability Assigned to True Event chart in the wikipedia article that NunoSempere linked. We've discussed supporting a spherical scoring rule to make the reward/penalty more symmetrical, but haven't pulled the trigger on it thus far.
Thanks Ben, this is interesting. I think we disagree somewhat on the extent to which relative Brier avoids the question selection problem (see Nuno's comment on this), and also whether it's desirable to award no points for agreeing with the crowd, but I definitely think the case for relative Brier being the best option is reasonable and that you have made it well.
I'm interested in particular in your comment on extremising meaning that it's possible that the overconfidence incentive in some tournament scoring is desirable. My understanding is that the qualitative argument for extremising being useful is that if several people independently rate an event as being almost certain, they may have different reasons for doing so. It seems that the benefit of extremising may be much smaller, and possibly non-existent, if a crowd can see the aggregate forecast, possibly moreso if the crowd can see every individual forecast that's been made. Do you know of any research on this? I'd be interested to see some.
As far as I know, the Metaculus algorithm does not "deliberately" extremise, however the exact procedure is not public, and it did recently produce a very confident set of predictions!
Re: question selection - I agree that there are some edge cases where the scoring system doesn't have perfect incentives around question selection (Nuno's being a good example). But for us, getting people to forecast at all in these tournaments has been a much, much bigger problem than any question selection nuances inherent in the scoring system. If improving the overall system accuracy is the primary goal, we're much more likely (IMO) to get more juice out of focusing time/resources/effort on increasing overall participation.
Re: extremizing - I haven't read specific papers on this (though there are probably some out there from the IARPA ACE program, if I had to guess). This might be related, but I admit I haven't actually read it :) - https://arxiv.org/pdf/1506.06405.pdf
But we've seen improvements in the aggregate forecast's Brier score if we apply very basic extremization to it (ie. anything <50% gets pushed closer to 0, anything above 50% gets pushed closer to 100%). This was true even when we showed the crowd forecast to individuals. But I'll also be the first to admit that connecting this to the idea that an overconfidence incentive is a good thing is purely speculative and is not something we've explicitly tested/investigated.
In the particular example you propose, forecaster A assigns higher probability to X and Y and Z (0.7*0.7*0.7 = .343) than forecaster B (0.8*0.8*0.5 = 0.320). This seems intuitively correct.
Also, note that the squares are necessary to keep the scoring rule proper (the highest expected reward is obtained by reporting the true probability distribution), and this is in principle a crucial property (otherwise people could lie about what they think their probabilities are and get a better score). In particular, if you take out the square, then the "probability" which maximizes your expected score is either 0% or 100% (i.e., imagine that your probability was 60%, and just calculate the expected value of writing 60% vs 100% down).
An alternative to the Brier score which might interest you (or which you may have had in mind) is the logarithmic scoring rule, which in a sense tries to quantify how much information you add or substract from the aggregate. But it has other downsides, like being very harsh on mistakes. And it would also assign a worse score to forecaster B.
What's the issue with this? Isn't this exactly what we want, to incentivize people to correct bad predictions? This gets us closer to prediction/betting markets.
Perhaps this should have been "you are incentivized to only pick questions for which you think the aggregate is particularly wrong" (according to the distance implied by your scoring rule), and neglect other questions. Essentially, it's the same problem as for the raw brier score:
but one step removed.
This is particularly noticeable and egregious in the case of important questions for which the probability is very low, for example Will China's Three Gorges Dam fail before 1 October 2020?, where the difference between ~0% and 3% is important back in reality. But predicting on this question will lower your Brier score difference (because if you think it's ~0%, the difference in Brier score will be very small; 0%=>0 vs 3%=>0.0018, where good forecasters tend to have much higher differences.)
One solution we tried at some foretold experiments was to pay out more (in the Brier score case, this would correspond to multiplying the brier score difference from the aggregate by a set amount) for questions we considered more important, so that even correcting smaller errors would be worth it.
Note that prediction markets still have a similar problem, where transactions fees and interest rates also mean that if the error is small enough you are also not incentivized to correct it.
Nuño might have additional thoughts, but I have a couple of concerns here.
It's possible to run into the following issues even (/especially) when people are "playing perfectly", at least in terms of trying to maximise points:
Somewhat seperately, I think this particular scoring system risks people making some bad decisions from both a points perspective and a good forecasting perspective:
Edit: I re-ordered the points above in order to try to be more clear, not all of them are concerned about exactly the same thing.
This shouldn't be a problem in the limit with a proper scoring rule.