EA Forum Bot Site
EA Forum

Jérémy A🔸

Head of Research @ GPAI Policy Lab
120 karmaJoined Working (0-5 years)49 Bd Diderot, 75012 Paris, France
Interests:
ResearchResearch careersCause prioritizationAcademiaBiosecurityPandemic preparednessAI safetyRethink PrioritiesEffective ThesisAI governanceForecastingAI forecasting

Bio

Participation
3

I'm Head of Research at the General-Purpose AI Policy Lab, a French AI Security organization, after a PhD in evolutionary biology modeling.

I cofounded EffiSciences, an organisation building talent pipelines and promoting mission-driven research in France and I'm currently on the Board of Effective Thesis.

I've also enjoyed exploring some Biosecurity projects (writing a "Critical review of modelling strategies against pandemics", contributing to Biosecurity.world).

How others can help me

Generally speaking, I'm looking forward to meeting new people and discussing AI policy, biosecurity, meta-research or your areas of interest!

I’m always looking for potential collaborators/interns for our modeling and forecasting projects. 
 

How I can help others

I'm happy to present the work we are doing at the GPAI Policy Lab, and the factors that make some of our actions particularly effective. I can also share my experience in starting up a nonprofit.

In the same vein, I have many thoughts on the impact of academic research and how to develop talent pipelines in universities.

Comments
2

Probability distributions of Cost-Effectiveness can be misleading
Jérémy A🔸8
0
0
1

Thanks for raising this question! Following other comment, I find the use of  somewhat unsatisfactory.

Perhaps some of the confusion could be reduced by i) taking into account the number of interventions and ii) distinguishing the following two situations:

1. Epistemic uncertainty: the magic intervention will always save 1 life, or always save 100 lives, or always save 199 lives, we just don't know. In this case, one can repeat the intervention as many times as one wants, the expected cost-effectiveness will remain ~$3,400/life.

2. True randomness: sometimes the magic intervention will save 1 life, sometimes 100 lives, sometimes 199 lives. What happens then if you repeat it n times? If , your expectation is still ~$3400/life (tail risk of a single life saved). But the more interventions you do, the more you converge to a combined cost-effectiveness $100/life (see figure below), because failed interventions will probably be compensated by very successful ones.

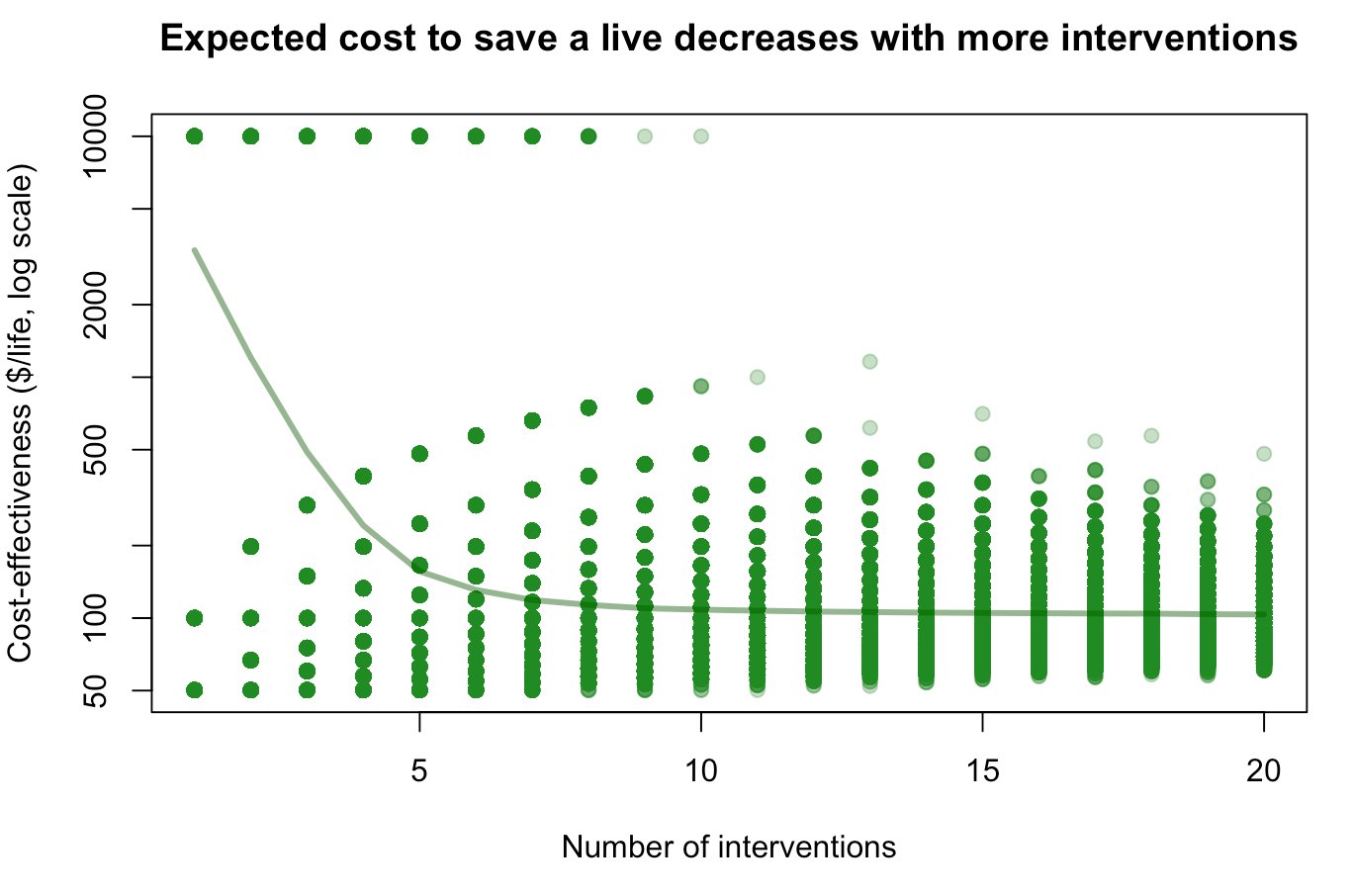
(R code to reproduce the plot : X <- sample(1:20,1000000, replace=T) ; Y <- sapply(X,function(n)mean(10000*n/sum(sample(c(1,100,199), n, replace = T)))) ; plot(X, Y, log="y", pch=19, col=alpha("forestgreen", 0.3), xlab="Number of interventions", ylab="Cost-effectiveness ($/life, log scale)", main="Expected cost to save a live decreases with more interventions") ; lines(sort(unique(X)), sapply(sort(unique(X)), function(x)mean(Y[X==x])), lwd=3, col=alpha("darkgreen",0.5)))

I'm not sure how to translate this into practice, especially since you can consider EA interventions as a portfolio even if you don't repeat the intervention 10 times yourself. But do you find this framing useful?

Reply