I've written a new paper some of you may be interested in. It was written in response to the problems arising in decision theory, economics, and ethics where standard approaches to evaluating an option leads to divergent sums or integrals. This makes it hard to evaluate and compare things like unending streams of value, when each option under consideration would standardly be assigned the value +∞. This leads theorists to develop a variety of conflicting approaches to making these comparisons and often even leads them to modify their theory of finite cases — adding things like a requirement for bounded utility or discounting of future utility in order to make the infinities go away.
I believe this problem is mainly caused by the use of the extended reals, which are an impoverished system of infinite numbers which is obviously not expressive enough to solve the problem. I show that once we switch to a number system that is expressive enough (the hyperreal numbers) and take the obvious generalisation of infinite sums and integrals to hyperreal values, that we immediately have a theory that can do most of the evaluation and comparison required. Here are some examples of the hyperreal valuations of some sums and integrals that would all standardly be evaluated as +∞
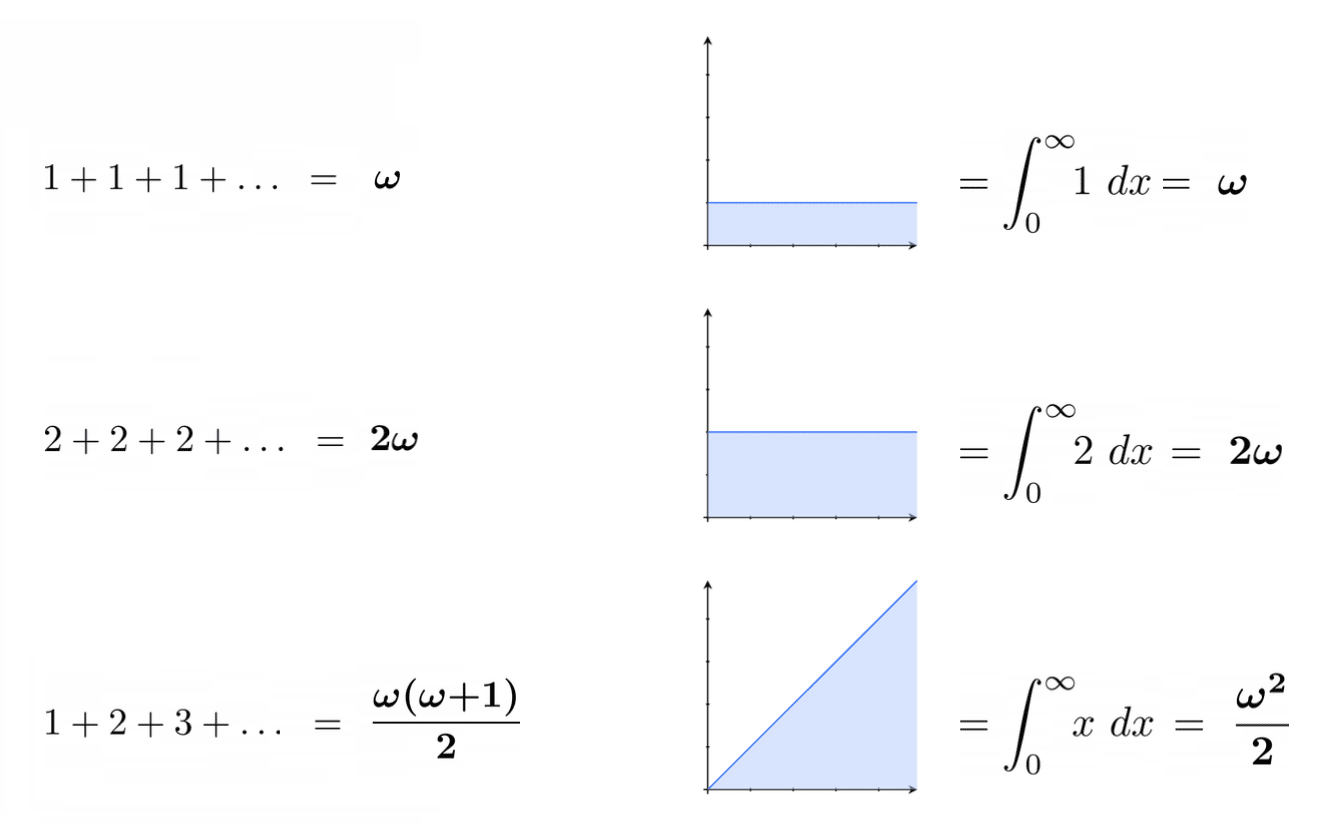
Using this method, when we compare options, we could find that one has value ω while another has value ω2, which while still infinite is only half as valuable. And that removing a single unit of value from a person in the latter option takes its value to ω2−1, which is worse by 1 unit as we would hope.
This new theory has implications in statistics (helping us work with distributions whose mean or variance is infinite), decision theory (allowing comparison of options with infinite expected values), economics (allowing evaluation of infinitely long streams of utility without discounting), and ethics (allowing evaluation of infinite worlds).
And it also has important implications for finite cases, since the ability to handle these infinities undermines a common argument for bounded utility, and the discounting of future utility. Altering our own values about finite cases in order to sidestep a technical issue about infinite cases should have been an absolute last-resort. Since the technical problem appears to have a technical solution, it looks like we can keep many of our intuitive values intact. For example, we can think a harm matters just as much regardless of when it occurs.
That said, my method doesn't attempt to solve all problems of infinite ethics and it does have some remaining issues, which I clearly outline in the paper.
My method applies to cases where we are evaluating an infinite whole in terms of its parts. This could be a prospect with infinitely many possible outcomes, a future with infinitely many years, or a universe with infinitely many inhabited planets. All theories assessing such infinite wholes in terms of their parts face a dilemma — they can only choose one of:
Pareto: improving every part of the whole must make the whole better
Unrestricted Permutation: a whole with the same parts but in a different order would be equally valuable.
So theories tackling this subject can be divided into two classes based on which of these principles they keep. Mine sides with Pareto.
A major theme in my results is that most of the counterintuitive aspects of the infinite are revealed to be artefacts of infinite number systems that are too coarse-grained and so are forced to lump together quite different things. On my theory, there is none of this ∞+1=∞ business where finite changes cease to make outcomes better or worse, or where a 50% chance of an infinite outcome is worth the same as a guarantee of that outcome, or where Hilbert-hotel-like rearrangements produce counterintuitive effects. Instead, the infinite behaves very much like the finite. Infinite values are much like any other value, except that they happen to be larger than all finite ones.
Thanks Toby, I think this is a useful write up! A random take that I've been meaning to write is that all "reasonable" aggregation methods are equivalent to a hyperreal utility function in the following sense:
If you aggregate persons through some mechanism ⊕ which meets the criteria for an abelian linearly ordered group, then there exists some hyperreal-valued utility function u such that ⨁ixi⪰⨁iyi⇔∗∑iu(xi)≥∗∑iu(yi).
Proof sketch:
The Hahn embedding theorem tells us that any abelian linearly-ordered group G=(G,⊕,⪰) can be order embedded into H=(RN,+,≥), where N is the (possibly infinite) number of Archimedean equivalence classes (i.e. "sizes of infinity") in G, ⊕,⪰ are some unknown aggregation and comparison mechanisms, respectively, + is normal element-wise addition and ≥ is lexicographical ordering (wlog assume it's right-to-left). We can, in turn, order-embed H into R∗ through ϕ(h0,h1,˙)=h0+h1ω+… provided that N is not larger than the largest ordinal in R∗. It's clear that this is order-preserving since the way you order the hyperreals is by first comparing the largest "infinity", then the second largest infinity, and so on.
Say the first embedding is ψ and let u=ϕ∘ψ; u is then our desired utility function, since the group structure gives us that u(⨁ixi)=∗∑iu(xi). ■
Corollary:
In the case when G is Archimedean (i.e. has no "infinite" elements), this just gives us classical (real-valued) utilitarianism: ⨁ixi⪰⨁iyi⇔∑iu(xi)≥∑iu(yi).
Commentary:
I think there are some technical details to be worked out (e.g. ensuring that the order-type of H actually matches the order-type of a subgroup of R∗) but think it probably works?[1] I expect that the controversy comes from the claim that the group axioms are actually reasonable: particularly the assumption that for any population x there exists some population −x such that x⊕−x=0 is something that I think many utilitarians believe but maybe others don't.
ChatGPT says this proof sketch is valid but that it is more natural to use Hahn series instead of the hyperreals. Its proof does seem more elegant at a quick skim, but I didn't look closely. Possibly a follow up paper could be about the use of Hahn series in infinite ethics?
Interesting! So this is a kind of representation theorem (a bit like the VNM Theorem) but instead of saying that Archimedean preferences of gambles can be represented as a standard sum, it says that any aggregation method (even a non-Archimedean one) can be represented by a sum of a hyperreal utility function applied to each of its parts.
In the paper you discuss how your approach to infinite utilities violates the continuity axiom of expected utility theory. But in my understanding, the continuity axiom (together with the other VNM axioms) provide the justification for why we should be trying to calculate expectation values in the first place. If we don't believe in those axioms, then we don't care about the VNM theorem, so why should we worry about expected utility at all (hyperreal or not)?
Is it possible to write down an alternative set of plausible axioms under which expected hyperreal utility maximization can be shown to be the unique rational way to make decisions? Is there a hyperreal analogue of the VNM theorem?
I think there is a version of VNM utility that survives and captures the core of what we wanted: i.e. a way of representing consistent ways of ordering prospects via cardinal values of individual outcomes — it it is just that these value of outcomes can be hyperreals. I really do think the 'continuity' axiom (which is really an Archimedean axiom saying that nothing is infinitely valuable compared to something else) is obviously false in these settings, so has to go (or to be replaced by a version that allows infinitesimal probabilities). I know that this axiom was important in deriving the real-valued representation of the utility functions (which I also need to be false), but am not sure what its role is in justifying valuing prospects by their means. I assume there are other ways to get there and don't think dropping/modifying the axiom will lead to circularity, but it may require some care to check.
One possibility is this: I don't value prospects by their classical expected utilities, but by the version calculated with the hyperreal sum or integral (which agrees to within an infinitesimal when the answer is finite, but can disagree when it is divergent). So I don't actually want the classical expected utility to be the measure of a prospect. It is possible that the continuity axiom gets you there and my modified or dropped version can allow caring about the hyperreal version of expectation.
You say "removing a single unit of value from a person in the latter option ... is worse by 1 unit as we would hope", but don't the ordering effects get very tricky?
For example, imagine everyone ever to live has a lifetime utility of 1, population size is constant, and so the utility of all future people is 1 + 1 + 1 + 1 ... = ω. But if I took some living person today and zeroed out their utility, then we might have 1 + 0 + 1 + 1 ... which is still ω in your formulation, no? And we'd prefer it to be ω - 1?
On the hyperreal approach 1 + 0 + 1 + 1 + … does actually equal ω−1 as desired.
This is an example of the general fact that adding zeros can change the hyperreal valuation of an infinite sum, which is a property that is pretty common in variant summation methods.
The short answer is that if you take the partial sums of the first n terms, you get the sequence 1, 1, 2, 3, 4, … which settles down to have its nth element being n−1 and thus is a representative sequence for the number ω−1. I think you'll be able to follow the maths in the paper quite well, especially if trying a few examples of things you'd like to sum or integrate for yourself on paper.
(There is some tricky stuff to do with ultrafilters, but that mainly comes up as a way of settling the matter for which of two sequences represents the higher number when they keep trading the lead infinitely many times.)
Executive summary: The post introduces a new paper arguing that many paradoxes in decision theory, economics, and ethics involving infinities can be resolved by replacing the extended reals with hyperreal numbers, which allow more nuanced evaluation and comparison of infinite sums and integrals, preserving intuitive values without resorting to discounting or bounded utility.
Key points:
Standard use of the extended reals forces divergent sums/integrals to collapse into +∞, which obscures meaningful comparisons and pressures theorists to artificially constrain models (e.g., bounded utility, discounting).
Hyperreal numbers provide a richer framework, enabling natural comparisons of infinite values (e.g., distinguishing between ω and ω², and allowing finite changes to matter).
The method has implications for statistics (handling infinite means/variances), decision theory (infinite expectations), economics (infinite utility streams), and ethics (evaluating infinite worlds).
By resolving the technical issue, the approach supports keeping intuitive stances on finite cases (e.g., harms matter equally regardless of when they occur) rather than distorting them to sidestep infinities.
The theory preserves the Pareto principle but not unrestricted permutation, and shows that many counterintuitive “infinite paradoxes” arise from overly coarse number systems.
Remaining issues are acknowledged, but the central result is that infinities can be treated in ways that behave much like finite values, avoiding paradoxes like ∞ + 1 = ∞ or Hilbert-hotel rearrangements.
This comment was auto-generated by the EA Forum Team. Feel free to point out issues with this summary by replying to the comment, andcontact us if you have feedback.
Interesting. Previously this was a major criticism I had of utilitarianism. The fact that the order of summing infinite series matters still seems like a big remaining problem.
I used AI to fix transcription errors, rerrarange the ideas, and suggest tweaks to the title and some sentences.
Three of the most exciting projects to come out of EA in recent years are, in a vague sense, CEA spinouts:
* Kairos is directly a spinout of CEA and now handles most support for university AI safety groups. Basically everyone I've found who knows them is really excited about what they do
* NEST is an opinionated ideas-fi...
TLDR; To help the effective animal advocacy movement cost-effectively absorb greater amounts of funding in the near future, we are seeking expressions of interest from people who could found a new organization focused on:
* Highly neglected animals: insects, wild animals, shrimp, fish, etc, or
* AI and animals: AI alignment and governance for animal welfare, strategic actions considering transformative AI, AI for wild animals, etc.
* ...
Thanks Toby, I think this is a useful write up! A random take that I've been meaning to write is that all "reasonable" aggregation methods are equivalent to a hyperreal utility function in the following sense:
Proof sketch:
The Hahn embedding theorem tells us that any abelian linearly-ordered group G=(G,⊕,⪰) can be order embedded into H=(RN,+,≥), where N is the (possibly infinite) number of Archimedean equivalence classes (i.e. "sizes of infinity") in G, ⊕,⪰ are some unknown aggregation and comparison mechanisms, respectively, + is normal element-wise addition and ≥ is lexicographical ordering (wlog assume it's right-to-left). We can, in turn, order-embed H into R∗ through ϕ(h0,h1,˙)=h0+h1ω+… provided that N is not larger than the largest ordinal in R∗. It's clear that this is order-preserving since the way you order the hyperreals is by first comparing the largest "infinity", then the second largest infinity, and so on.
Say the first embedding is ψ and let u=ϕ∘ψ; u is then our desired utility function, since the group structure gives us that u(⨁ixi)=∗∑iu(xi). ■
Corollary:
In the case when G is Archimedean (i.e. has no "infinite" elements), this just gives us classical (real-valued) utilitarianism: ⨁ixi⪰⨁iyi⇔∑iu(xi)≥∑iu(yi).
Commentary:
I think there are some technical details to be worked out (e.g. ensuring that the order-type of H actually matches the order-type of a subgroup of R∗) but think it probably works?[1] I expect that the controversy comes from the claim that the group axioms are actually reasonable: particularly the assumption that for any population x there exists some population −x such that x⊕−x=0 is something that I think many utilitarians believe but maybe others don't.
ChatGPT says this proof sketch is valid but that it is more natural to use Hahn series instead of the hyperreals. Its proof does seem more elegant at a quick skim, but I didn't look closely. Possibly a follow up paper could be about the use of Hahn series in infinite ethics?
Interesting! So this is a kind of representation theorem (a bit like the VNM Theorem) but instead of saying that Archimedean preferences of gambles can be represented as a standard sum, it says that any aggregation method (even a non-Archimedean one) can be represented by a sum of a hyperreal utility function applied to each of its parts.
Yes, I think that's a good summary!