Summary
- I think the prior probability of this being the most important century is less than 1 % based on i) the self-sampling assumption (SSA), ii) a loguniform distribution of the effective computation this century as a fraction of that throughout all time, and iii) all effective computation being more than 10^44 times as large as that this century.
- The bigger the influentialness of the future, the lower the probability of this century being influential.
Methods
In agreement with section 2 of Mogensen 2022, the self-sampling assumption (SSA) says the prior probability of being the most influential person among a population of size N, comprising past, present and future people, is the expected value of 1/N (not the reciprocal of the expected value of N). To be more general, I have estimated the prior probability of this being the most important century from the expected value of effective computation this century as a fraction of that throughout all time. By effective computation, I mean one which counterfactually increases/decreases welfare, regardless of whether it comes from biological beings or artificial intelligence (AI).
Artificial general intelligence (AGI) might soon cause lock-in to a certain extent. If this does not involve total loss of value[1], the vast majority of computation could still happen in the longterm future, but one would not be able to counterfactually increase/decrease welfare.
In addition, this might be the most important century owing to high risk of human extinction. However, a priori, one should arguably expect such risk to also be proportional to the expected value of effective computation this century as a fraction of that throughout all time. Along the same lines, I wonder whether the vast majority of technological progress will happen in the longterm future.
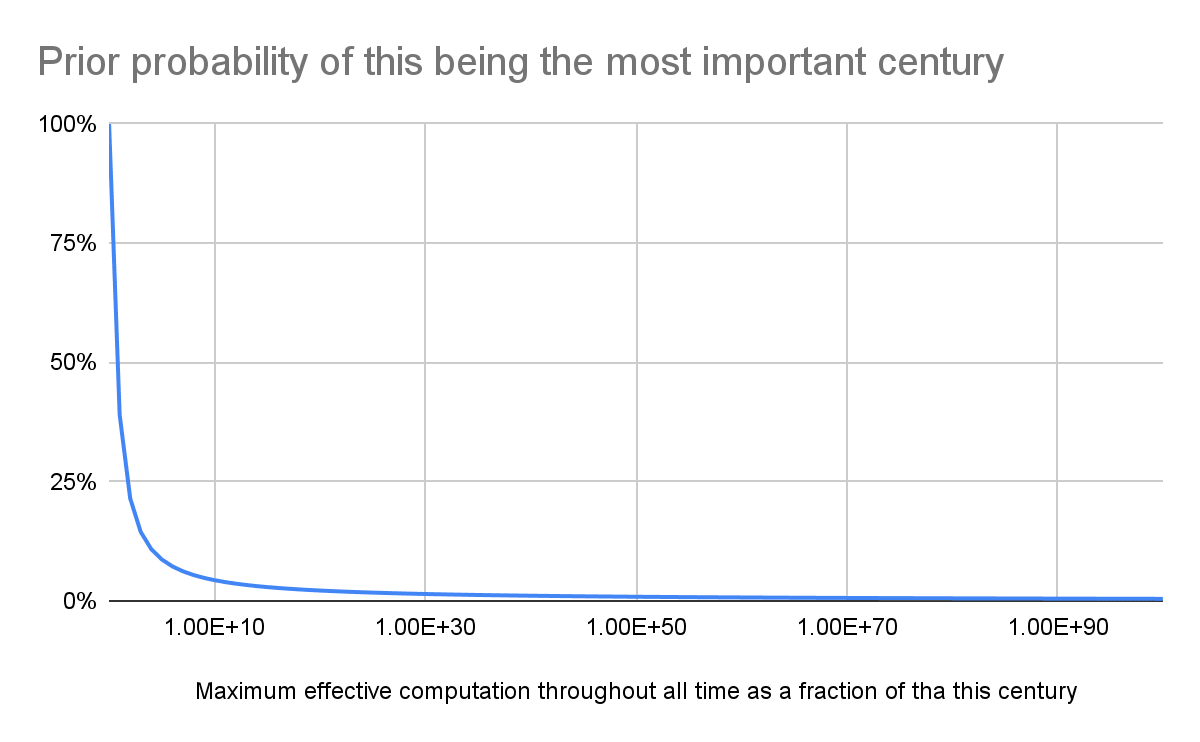
I modelled the effective computation this century as a fraction of that throughout all time as a loguniform distribution, which is a good uninformative prior. Its expected value is (b - a)/(ln(b) - ln(a)), where a and b = 1 are its minimum and maximum. As a approaches 0 for b = 1, the expected value tends to 1/ln(1/a). In other words, the prior probability of this being the most important century is inversely proportional to the logarithm of the maximum effective computation throughout all time as a fraction of that this century. The bigger the influentialness of the future, the lower the probability of this century being influential.
Results
The results are below. My calculations are in this Sheet.
Discussion
The future can hold at least as many as 10^54 lives according to Newberry 2021 (Table 1), and this century can have less than 10 billion (10^10) lives. Consequently, 1/a is lower than 10^(54 - 10) = 10^44, which suggests a prior probability of this being the most important century of less than 0.987 %.
Note I would have (wrongly) arrived at a much lower probability based on the reciprocal of the expected effective computation throughout all time as a fraction of that this century. For the conservative estimate of 10^28 expected future lives given in Newberry 2021 (Table 3), which is at least 10^(28 - 10) = 10^18 times as many as the lives this century, I would get a prior probability of 10^-18. Much lower than 1 %! 10^-18 is the kind of value which would result from following the formulation arguably implied in MacAskill 2020[2], but it is not in agreement with the SSA, as explained in section 2 of Mogensen 2022.
Acknowledgements
Thanks to David Denkenberger for feedback on the draft.
- ^
I do not think AGI causing human extinction would necessarily lead to a permanent loss of value.
- ^
William MacAskill provides numbers with respect to time. Consequently, since population size increases throughout time, all lives as a fraction of those this century is much smaller than all valuable time as a fraction of 100 years. So William gets a probability higher than 10^-18 for this being the most important century. Nevertheless, William agrees population is also relevant:
However, for the purposes of true action-relevance, the influentialness of a time is not quite what we’re looking for. Even if we assume that now is the most influential time, because there are available opportunities to safeguard the longrun future, a rural farmer in Central African Republic would simply not be able to access those opportunities, and so for that person the question of how influential the present time is is neither here nor there. So we can generalize Trammell’s model slightly by talking about person-times rather than times: rather than being indexed to a particular time, each term in his model should be indexed to a particular person-time [i.e. life].

Sure, you don't buy this but shouldn't you still account for it in your prior? or is this just "a prior if we discount extinction"?
Hi Nathan,
The prior is supposed to account for extinction risk.