Vasco Grilo🔸
Bio
Participation4
I am a generalist quantitative researcher. I am open to volunteering and paid work. I welcome suggestions for posts. You can give me feedback here (anonymously or not).
How others can help me
I am open to volunteering and paid work (I usually ask for 20 $/h). I welcome suggestions for posts. You can give me feedback here (anonymously or not).
How I can help others
I can help with career advice, prioritisation, and quantitative analyses.
Posts 215
Comments2660
Topic contributions36
Thanks for the comment, Noah.
I am looking forward to the results of RP's Digital Consciousness Project, but I do not expect any significant updates to my views. It focusses on the probability of consciousness, but I think this says very little about the (expected hedonistic) welfare per unit time. This is because I believe there is much more uncertainty in the welfare per unit time conditional on consciousness than in the probability of consciousness.
I suspect the number of digital minds is not among the most relevant parameters to track. It may not be proportional to total digital welfare because more digital minds will tend to have less individual welfare per unit time. I would focus more on the digital welfare per FLOP, and FLOPs per year.
I am also interested in more comparisons between the promise of increasing biological and digital welfare. Nice to know you are working on a piece!
Fair! What they mean is closer to "AI as a more normal technology than many predict". Somewhat relatedly, I liked the post Common Ground between AI 2027 & AI as Normal Technology.
For my assumed human performance of 10^15 FLOP/s, and human basal metabolic power of 80 W, the computational energy efficiency (operations per unit energy) of humans is 12.5 k GFLOP/J (= 10^15/80). This is 5.00 times (= 12.5*10^3/(2.5*10^3)) that of NVIDIA B100 (released on 15 November 2024), which is the ML hardware on Epoch AI's database with the highest computational energy efficiency. Epoch AI estimates the computational energy efficiency of ML hardware has increased 30 % per year, as is illustrated below. At this rate, ML hardware will reach the computational energy efficiency of humans in 6.13 years (= LN(5.00)/LN(1 + 0.3)). As a result, digital welfare per unit energy consumption will soon be similar to human welfare per unit energy consumption if digital welfare per FLOP is similar to human welfare per FLOP.
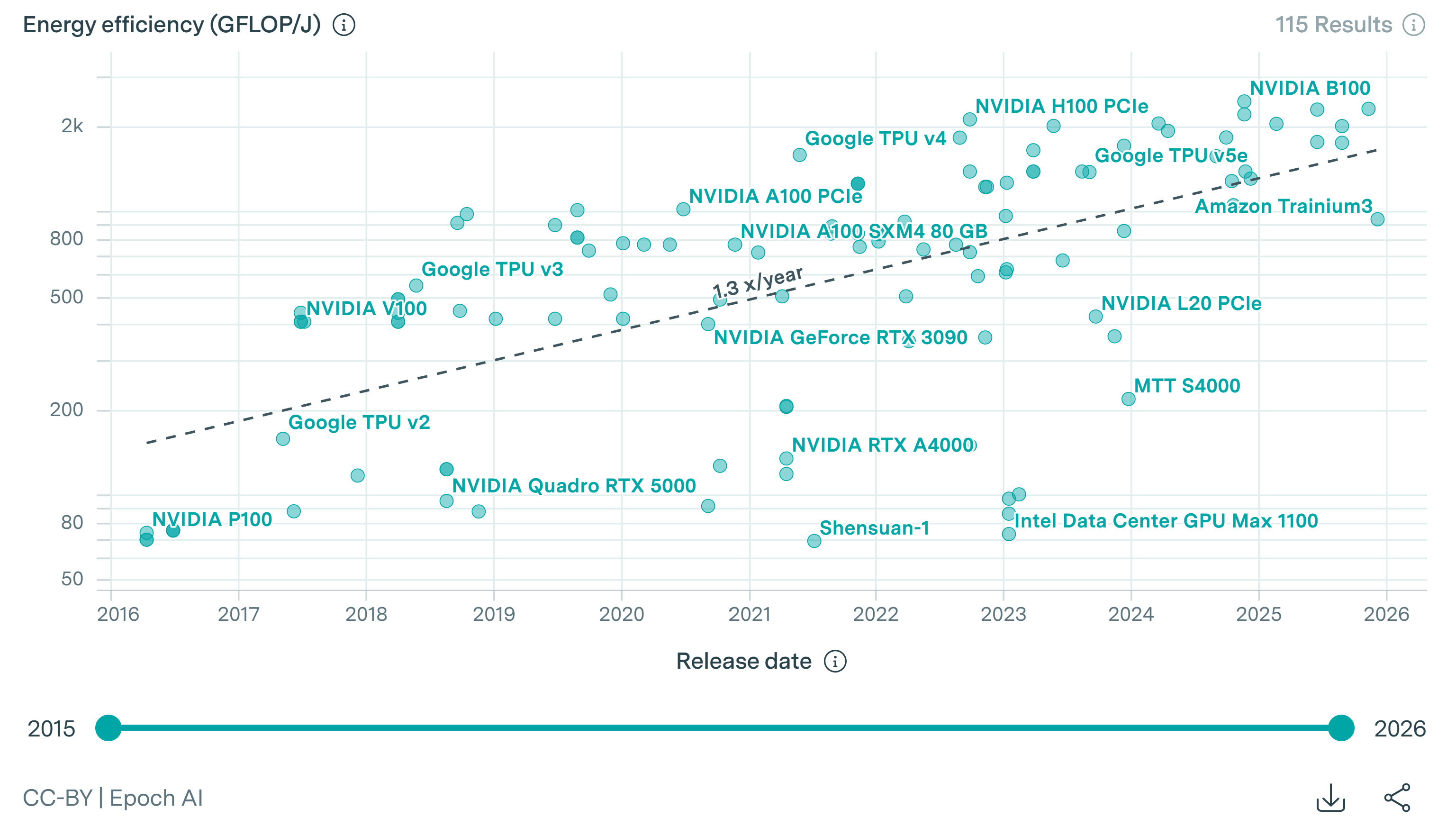
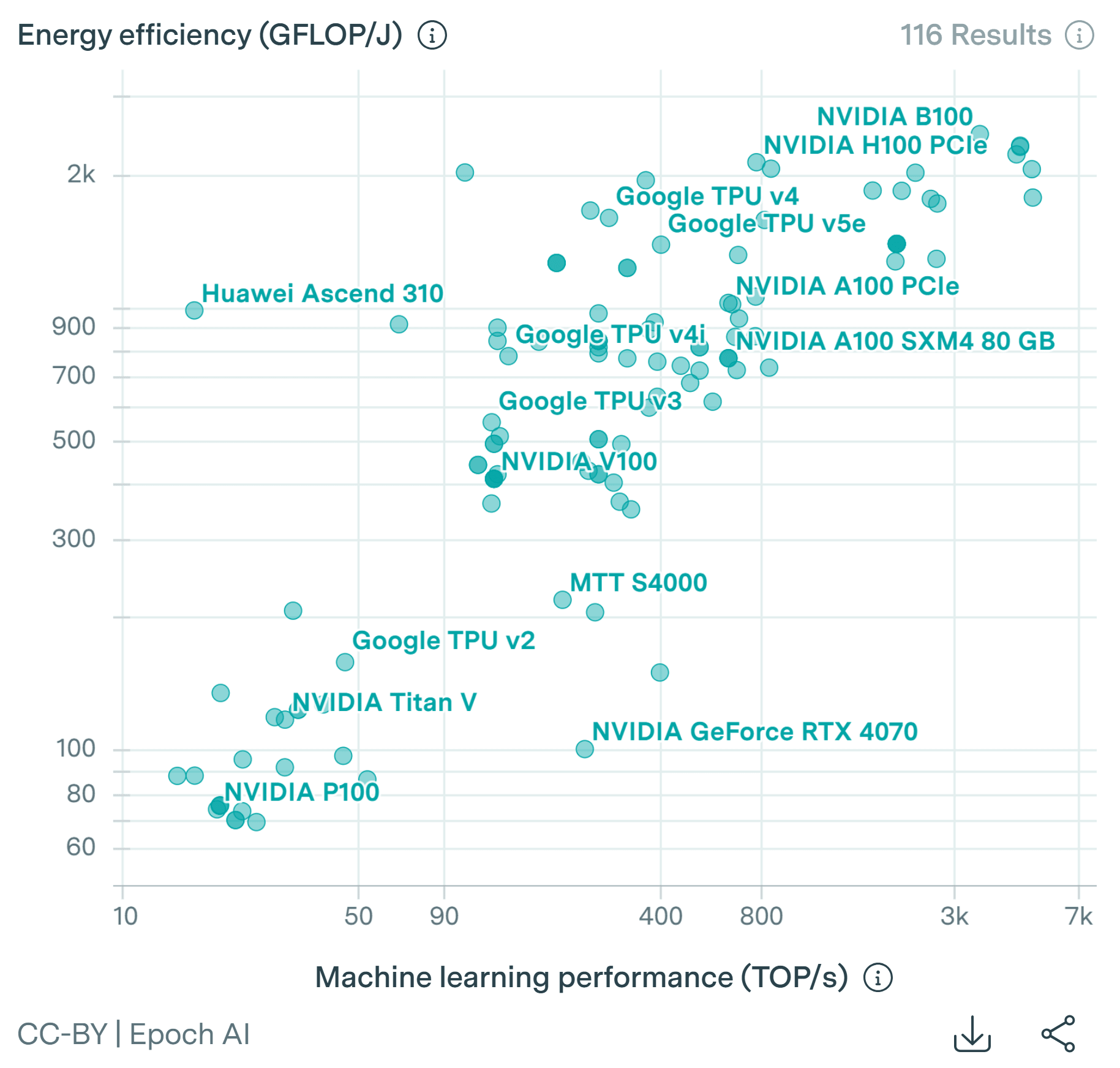
Computational energy efficiency tends to increase with performance, as is illustrated by the data below collected by Epoch AI. I assume organisms with a smaller individual mass tend to have lower performance. So I think humans have a higher computational energy efficiency than animals, and that these have a higher one than microorganisms.
Thanks for the questions, Huw!
In your opinion, if C. Elegans is conscious and has some moral significance, and suppose we could hypothetically train artificial neural networks to simulate a C. Elegans, would the resulting simulation have moral significance?
I would say the moral significance, which for me is the expected hedonistic welfare per unit time, of the simulation would tend to that of the C. Elegans as more components of this were accurately simulated. I do not think perfectly simulating the behaviour is enough for the moral significance of the simulation to match that of the C. Elegans. I believe simulating some of the underlying mechanisms that produced the behaviour may also be relevant, as Anil Seth discussed on The 80,000 Hours Podcast.
Consciousness does not necessarily imply valenced (positive or negative) subjective experiences (sentience), which is what I care about (I strongly endorse hedonism). C. Elegans being conscious with 100 % probability would update me towards them having a greater probability of being sentient, but not that much. I am mostly uncertain about their expected hedonistic welfare per unit time conditional on sentience, not about their probability of sentience. I would say everything, including a Planck volume in deep space vacuum, could have a probability of sentience of more than, for example, 1 % if it is operationalised in a very inclusive way. However, more inclusive operationalisations of sentience will lead to a smaller expected hedonistic welfare per unit time conditional on sentience. So I would like discussions of moral significance to focus on the expected hedonistic welfare per unit time instead of just the probability of sentience, or just the expected hedonistic welfare per unit time conditional on sentience.
If so, what other consequences flow from this—do image recognition networks running on my phone have moral significance? Do LLMs? Are we already torturing billions of digital minds?
I think increasing the welfare of soil animals will remain much more cost-effective than increasing digital welfare. Assuming digital welfare per FLOP is equal to the welfare per FLOP of a fully healthy human, I calculate the price-performance of digital system has to surpass 2.23*10^27 FLOP/$ for increasing digital welfare to be more cost-effective than increasing the welfare of soil animals, which corresponds to doubling more than 29.0 times starting from the highest one on 9 November 2023. One would need 60.9 years for this to happen for Epoch AI’s doubling time of the FP32 price-performance of machine learning (ML) hardware from 2006 to 2023 of 2.1 years.
Welcome to the EA Forum, Shloka! Thanks for the great comment. I strongly upvoted it.
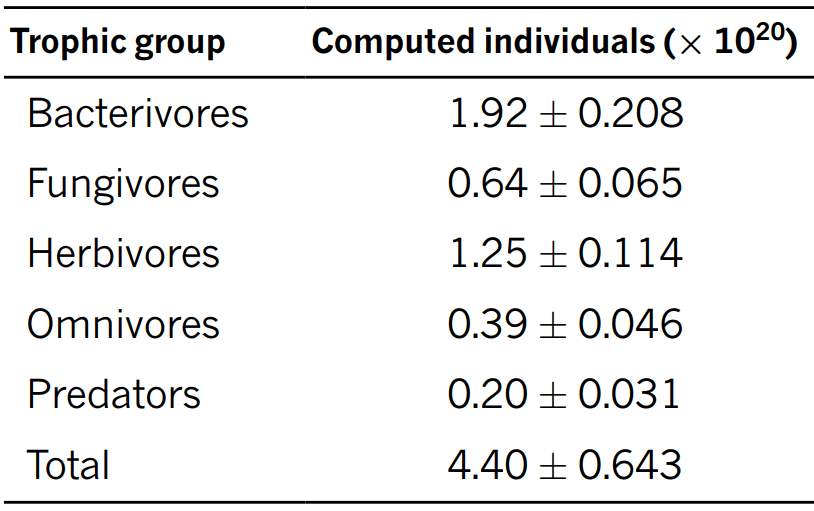
I have not looked into the effects of land use change on different groups of nematodes. From Table 1 of van den Hoogen et al. (2019), which is below, the most abundant soil nematodes are bacterivores and herbivores, so I speculate effects on these are the most important. However, I agree a given land use change may increase the welfare of nematodes of a given type, but decrease that of ones of a different type. This strengthens my conclusion that the priority is research informing how to increase the welfare of soil animals, not pursuing whatever land use change interventions naively seem to achieve that the most cost-effectively.
Hi Abraham.
I think the opportunity for impact for wild animal welfare is way bigger, and it's much more "normal"
I agree the absolute value of the total welfare of wild animals is much larger than that of farmed animals. On the other hand, the most popular opportunities to help wild animals focus on ones which only account for a small fraction of the total welfare of wild animals (although I think they change the welfare of soil animals much more). In extreme cases, such opportunitites would only improve the welfare of a few wild mammals to avoid the extinction of species. Of course, this is not the target of the Center for Wild Animal Welfare (CWAW), or Wild Animal Initiative (WAI). However, I still wonder about whether CWAW and WAI are focussing too much on what is popular, and underfunding research informing how to increase the welfare of (wild) soil animals. I currently think funding the Arthropoda Foundation is the best option for this. Mal Graham, who together with Bob Fischer "make[s] most of the strategic and granting decisions for Arthropoda", mentioned "We collaborate with Wild Animal Initiative (I’m the strategy director at WAI) to reduce duplication of effort, and have a slightly better public profile for running soil invertebrate studies, so we expect it will generally be Arthropoda rather than WAI who would be more likely to run this kind of program".

Thanks for the interesting points, Noah.
I said in the post "I analyse the cost-effectiveness of increasing the welfare of soil animals via funding HIPF, which is the most cost-effective way of increasing welfare I am aware of". This was for my best guess at the time that increasing agricultural land increases welfare due to decreasing the number of soil animals, and these having negative lives. However, I am now very uncertain not only about whether soil animals have positive or negative lives, but also about whether increasing agricultural land decreases or increases the number of soil animals. I recommend research informing how to increase the welfare of soil animals over pursuing whatever land use change interventions naively seem to achieve that the most cost-effectively. In addition, I would prioritise more research on comparing the hedonistic welfare of different potential beings (animals, microoranisms, and AIs).
I estimated the cost-effectiveness of HIPF assuming "the [expected hedonistic individual] welfare per animal-year of soil ants/termites/springtails/mites/nematodes is -25 % that of fully happy soil ants/termites/springtails/mites/nematodes". The expected cost-effectiveness only depends on the mean of the distribution of the individual welfare per animal-year as a fraction of that of fully happy animals. So one could have my best guess for the mean of this distribution while being arbitrarily uncertain. For example, a normal distribution with 5th and 95th percentiles of -5.25 (= -0.25 - 5) and 4.75 (= -0.25 + 5) would have a mean of -0.25 (my best guess), standard deviation of 11.1 (= 2*5/(0.95 - 0.05)), and probability of being negative of 50.9 % (= NORMDIST(0, -0.25, 11.1, 1)), which seems reasonable to me. A normal distribution with 5th and 95th percentiles of -50.25 (= -0.25 - 50) and 49.75 (= -0.25 + 50) would have the same mean of -0.25, standard deviation of 111 (= 2*50/(0.95 - 0.05)), and probability of being negative of 50.1 % (= NORMDIST(0, -0.25, 111, 1)). This is 9.00 (= (0.509 - 0.5)/(0.501 - 0.5)) times as close to 50 % as the probability of the 1st distribution being negative, but the expected cost-effectiveness would be the same for both distributions. What changes is that the cost-effectiveness of decreasing the uncertainty about whether soil animals have positive or negative lives is higher for the 2nd distribution.