To recap, first, we face an epistemic challenge beyond uncertainty over possible futures. Due to unawareness, we can’t conceive of many relevant futures in the first place, which makes the standard EV framework ill-suited for impartial altruistic decision-making. And second, we can’t trust that our intuitive comparisons of strategies’ overall consequences price in factors we’re unaware of with enough precision. We’ll need to evaluate these consequences with a framework that explicitly accounts for unawareness, that is, unawareness-inclusive expected value (UEV).
Here, I’ll more specifically unpack the UEV model, and argue that we can’t compare the UEV of any given strategy with another. If so, we don’t have a reason to choose one strategy over another based purely on the impartial good. We should, instead, suspend judgment as far as impartial altruism is concerned. I’ll conclude by illustrating this problem with a worked example, building on our case study from before. (My arguments here aren’t meant to refute the specific approaches EAs have proposed for comparing strategies under unawareness. That’s for the final post.)
Unawareness-inclusive expected value (UEV)[1]
Key takeaway
To get the imprecise “EV” of a strategy under unawareness, we take the EV with respect to all plausible ways of precisely evaluating coarse outcomes.
Where exactly does the UEV for a given strategy come from? As we might remember, the kinds of possibilities we conceive of are coarse-grained descriptions of many possible worlds, called hypotheses. So let’s construct a rough model that reflects the imprecision of our understanding of these hypotheses, taking inspiration from imprecise probabilities (i.e., representing beliefs with a set of probability distributions).
This will get a bit technical, but here’s the TL;DR:
- Instead of pinning down a unique list of values for every hypothesis, we consider multiple ways of assigning precise values consistent with our evidence and principles. (E.g., to evaluate the hypothesis “misaligned ASI takes over”, we could entertain a range of more specific — though still coarse-grained — misalignment scenarios.)
- Aren’t these precise values, too, arbitrary? Indeed. This model is meant to be merely the least bad formalization of our vague epistemic state (as discussed in the imprecision FAQ).
- To compute a strategy’s UEV, we compute the EV with respect to all these precise value assignments.
- One strategy is better than another if and only if it has higher EV for every precise value assignment.
Now let’s make this outline more rigorous (see Appendix B for more) and see more of the motivation for each step. We’ll look at a concrete application of this model later.
Step 1. Let’s call the set of all hypotheses we’re aware of our awareness set. Take each hypothesis in our awareness set,[2] plus the catch-all hypothesis (“every possible world that isn’t covered by the hypotheses we’re aware of”). As a toy example, suppose our awareness set consists of:
- “misaligned ASI takes over”;
- “ASI aligned with relatively benevolent humans takes over”; and
- “ASI aligned with relatively malevolent humans takes over”.
Step 2. For each , we represent different ways of making precise via a set of fine-grainings, which are rough approximations of possible worlds that describes. Taking “misaligned ASI takes over” as our example, this might include sub-hypotheses like:
- “misaligned ASI takes over and tiles the lightcone with paperclips”;
- “misaligned ASI takes over but gives humans 1% of the lightcone”; etc.
(Of course, we aren’t literally aware of the corresponding possible worlds themselves. But we use these approximations to reason about the value under a coarse hypothesis (that is, the value of the actual world supposing hypothesis is true).)
Step 3. Once we have our fine-grainings, we then assign a precise value to each fine-graining. However, to represent our inability to precisely weigh up the likelihoods of the fine-grainings, we have a set of probability distributions over the set of all fine-grainings of all hypotheses , conditional on our strategy . For simplicity, suppose our two sub-hypotheses from Step 2 represent all of our fine-grainings, where:
- one in assigns a weight of 0.8 to fine-graining (A), and 0.2 to (B); yet
- another assigns 0.2 to (A), 0.8 to (B).
Step 4. Finally, we compute the UEV: The UEV of is the set of EVs computed with respect to the values of these fine-grainings, under each distribution in (denoted ).
Comparing strategies under the UEV model
Key takeaway
Given two strategies, if neither strategy is net-better than the other under all these ways of making precise evaluations, then we’re not justified in comparing these strategies.
Since UEV is a set of EVs, not a number, it’s not obvious how to compare two strategies. At the very least, we can ask whether one strategy dominates the other, that is, whether it has higher EV under every precise distribution in . I claim that we can’t go further than dominance reasoning. Analogous to the maximality rule for decision-making with imprecise probabilities, we should say: Strategy is better than if and only if has higher under every in . If neither strategy is better than the other, nor are all the values exactly equal, then and are incomparable. (Interestingly, if we use this criterion, it’s not clear that “is this intervention positive?” is even the right question. See Appendix C.)
This condition for UEV comparisons might seem too permissive. We could try aggregating our set of probability distributions into one distribution, or aggregating the UEV interval. But as we saw in the imprecision FAQ, these moves would reintroduce the arbitrary precision we sought to avoid. (See footnote for why aggregating the UEV interval is problematic even if there’s a privileged way to aggregate.[3])
We don’t need to formally compute UEVs to choose a strategy. But remember, if our reason for choosing over is that we think has better overall consequences, we need an operationalization of “better overall consequences” that accounts for unawareness. And UEV (or similar[4]) seems like the most natural operationalization. I’ll discuss a possible alternative in the final post.
Reasons to suspend judgment on comparisons of strategies’ UEV
Key takeaway
Our evaluations of pairs of strategies should be so severely imprecise that they’re incomparable, unless we can argue for further constraints on their relative value.
(Credit to Jesse Clifton for the key points in the following two subsections.)
We’ve already seen some arguments for why our strategies’ UEV might be severely imprecise. But those arguments only refuted intuition-based UEV comparisons. Maybe more explicit UEV modeling can block the radical conclusion from the introduction, “we don’t have a reason to choose one strategy over another based purely on the impartial good”. For instance, Greaves and MacAskill (2021, Sec. 7.4) say:
[W]e don’t ourselves think that any plausible degree of imprecision in the case at hand will undermine the argument for strong longtermism. For example, we don’t think any reasonable representor [i.e., set of probability distributions representing our beliefs] even contains a probability function according to which efforts to mitigate AI risk save only 0.001 lives per $100 in expectation.
I think this sort of claim significantly understates the potential for interventions to backfire by impartial lights. Instead, I’ll argue that the murkiness of the catch-all, and the fact that even the hypotheses we’re aware of are very coarse, are strong grounds for severely imprecise UEVs.
Problem 1: Modeling the catch-all, and biased sampling
Key takeaway
Given the possibilities we’re aware of, there are very few constraints on how to precisely model the possibilities we’re unaware of. This lack of constraints is worsened by systematic biases in how we discover new hypotheses. For example, we may be disproportionately likely to consider hypotheses that we happen to find interesting.
The catch-all is (we may recall) a complex set of action-relevant possibilities we’re unaware of. How should we model this set? Given how blind we are to the contents of the catch-all, we might want to assume the catch-all has a precisely symmetric effect on any pair of strategies’ UEV. We’ll come back to that in the final post. For now, let’s see why we could just as well entertain various other precise models, hence, our all-things-considered model of the catch-all seems deeply underconstrained.
Consider your favorite intervention, let’s say, advocating for digital mind welfare. And imagine you become aware of some new pessimistic hypothesis. E.g., advocating for digital mind welfare could make it easier for misaligned AIs to take over by gaining humans’ sympathy (see Fenwick). Should you update toward more pessimism about the other possibilities in the catch-all? How much more?
To do a Bayesian update on “I became aware of [hypothesis]”, we need to form beliefs about our likelihood of becoming aware of different hypotheses, conditional on different possible contents of the catch-all. This is our first source of severe imprecision: When we discover new hypotheses, we should update our estimates of how the catch-all affects strategies’ UEV. But it’s very unclear how to do this.
Of course, it’s not as if we can specify likelihoods for Bayesian updates with exact precision, even in local-scale problems. On that scale, though, we can (recall again) at least get enough precision that our choices aren’t sensitive to this margin of error. Whereas here, we need to reason about how we explore a vast space of as-yet-undiscovered hypotheses, some of which could totally upend our current understanding. Where do the likelihoods for this come from? How do we non-arbitrarily pin them down to an action-guiding level of precision?
This brings us to the problem of biased sampling of hypotheses into awareness. Our hypothesis discovery process is, from the inside, extremely opaque. But it’s not hard to think of biases that could lead us to more often discover hypotheses that favor certain strategies over others. E.g.:
- A bias towards action might lead us to think of hypotheses that make interventions look good.
- Some kinds of (unendorsed) risk aversion or egoism might increase the salience of those that make interventions look bad.
Besides cognitive biases per se, the considerations that occur to us are filtered via personal interests, conversations and readings we happen to stumble upon, founder effects and information cascades in the EA/rationalist communities, and our inability to access information about other corners of the universe/multiverse.[5]
So, the distribution of hypotheses in the catch-all might differ from that of our awareness set, in various directions, and it’s far from clear how to weigh up these deviations. See Fig. 4 for a visualization of different possible catch-alls consistent with a given awareness set. This is a source of significant imprecision, even if our biases aren’t systematically optimistic about intervening. (And, no, we can’t say the biases subjectively cancel out because we don’t know their net direction; see the final post, here and here.) Not only are we looking under the streetlight, we’re looking under a streetlight that we have no particular reason to think we’ve sampled uniformly from the space of streetlights.
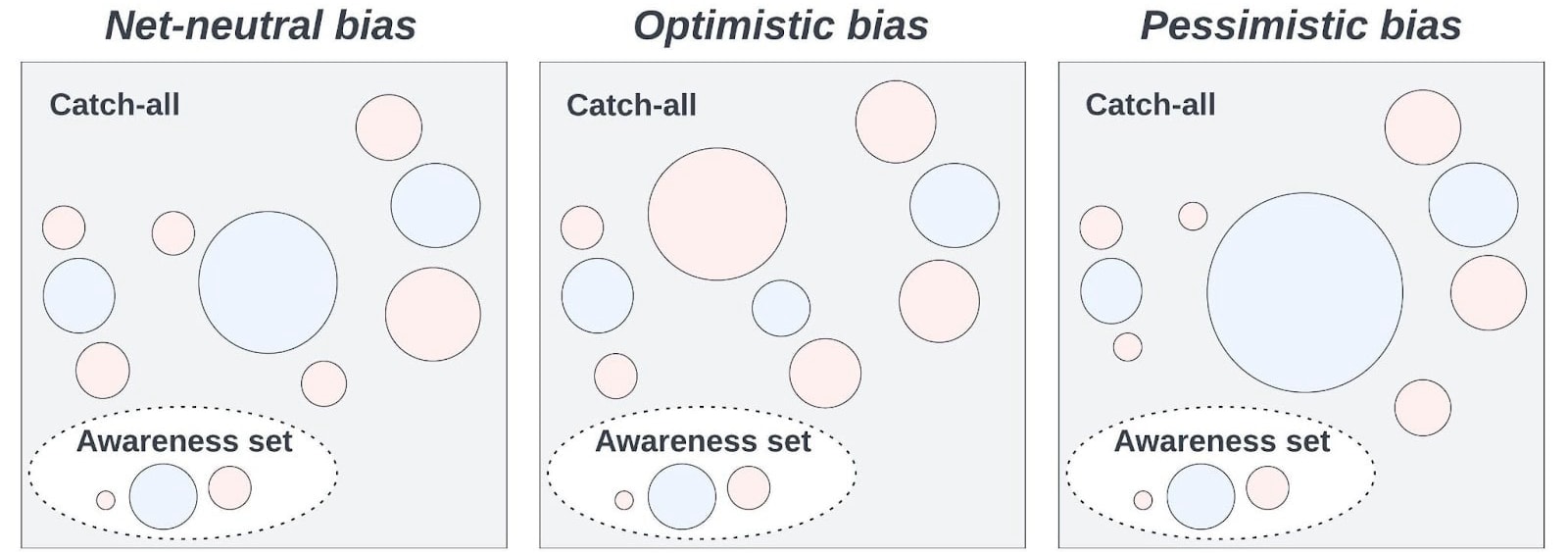 |
| Figure 4. Blue (resp. red) circles correspond to hypotheses under which some strategy is positive (resp. negative); size depicts the magnitude of the contribution of the hypothesis to the UEV. Based on the hypotheses we have access to and find salient (the awareness set), the strategy looks positive. If that set is a biased sample, however, various possible structures of the catch-all are consistent with the pattern in the awareness set. The overall bias could be roughly neutral, or highly optimistic, or highly pessimistic. And it’s not clear what the bias “in expectation” over these possibilities is. |
I’m not saying we should radically doubt all our beliefs because of our biases. Once more, the problem here stems from the unusual sensitivity to unawareness of our impartial net impact, compared to local goals. We should thus expect that when we model the catch-all’s effect on strategies’ UEV, these models will be highly sensitive to biased sampling. So it looks hard to avoid severely imprecise UEVs overall. How good or bad is digital minds advocacy supposing [insert crucial consideration we’re missing here]? Perhaps we can put some weak constraints on the answer, but beyond that? Who knows.
Problem 2: Severe underspecification of coarse hypotheses
Key takeaway
Suppose we try breaking down the space of possible outcomes into manageable categories. Since we can only break things down so far, the categories we can model remain too coarse-grained to pin down whether a strategy’s expected upsides outweigh its downsides.
As we’ve seen, the hypotheses we’re aware of are often very coarse. So there seem to be many ways of assigning precise values to these hypotheses, none of which is more justifiable than another. Nonetheless, we might think:
We can still cover all the practically relevant worlds in these hypotheses. For instance, we could try a logically exhaustive breakdown of strategically relevant categories (like “alignment succeeds, takeoff is multipolar, value lock-in is technically easy, and …”). Then, if the breakdown is fine-grained enough, each category shouldn’t have that much imprecision. Plus, this approach would solve the catch-all problem, since we’ve covered all possible futures.
The problem is that after we’ve broken the space down as much as we realistically can, our grasp on these categories will remain quite fuzzy. Even today, AI risk researchers feel the need to disentangle a concept as essential to our evaluation of possible futures as “alignment” (e.g., Carlsmith and Wentworth). And even with exhaustive categories, we need to reason about more specific scenarios to assign values to them — which means we’ll need “catch-alls” within each category.
For example, say we want to evaluate the sign of digital minds advocacy. We start partitioning the set of possible worlds using features like “difficulty of identifying sentience”, “default level of public sympathy for AI rights”, “default level of AI cooperativeness”, etc. The number of world categories increases exponentially with the number of features, as does the difficulty of specifying probability distributions over these categories. As cognitively bounded agents, we can only consider a few features.
And these features radically underconstrain the values we are to assign to each category, in particular, the relative strengths of the positive vs. negative effects. Try to weigh these up yourself. How good or bad is digital minds advocacy relative to inaction if, e.g.:
- it’s hard to tell whether a given AI system has the computational functions necessary(?) for valenced experiences;
- by default most people want humans to heavily control AIs, but they wouldn’t if they viewed them as persons; and
- misaligned AIs tend to be more cooperative (how much more?) with those who treat them well?
Despite breaking down the possibility space, we’re still unable to clearly conceive of the balance of optimistic vs. pessimistic scenarios. That is, in some scenarios, the (i) upsides of avoiding moral atrocities against AIs and promoting AI-human cooperation outweigh the (ii) risks of undermining AI control measures. In others, (ii) outweighs (i). Or what if sufficiently powerful misaligned AIs wouldn’t cooperate with humans anyway? It’s hard to see how, after reasoning through these possibilities without hand-waving, we could avoid a highly imprecise UEV.
Case study revisited: Sign indeterminacy of AI safety interventions due to unawareness
Let’s now dust off our old case study of AI control, to see what the UEV framework says about a concrete intervention all things considered. Of course, different interventions will be sensitive to unawareness in different ways. I invite you to try the following exercise for whichever intervention you favor. But I expect the lessons below to generalize, because the underlying pathologies aren’t specific to AI safety interventions. They’re precisely the same two structural problems we’ve just seen, i.e., challenges for modeling the catch-all and the severe coarseness of our hypotheses. I’ll start with the high-level diagnosis, then dig into the details.
What we’re missing: Outcome robustness and implementation robustness
Key takeaway
We have unawareness at the level of both (i) how good different world-states are (like “misaligned AIs take over”) relative to each other, and (ii) how effective concrete interventions are at steering toward vs. away from a given world-state.
(Credit to Anni Leskelä for coming up with this framework.)
Here’s the bottom line up front. The conventional longtermist recipe for managing massive uncertainty goes something like: Identify a high-stakes outcome we want to avoid, thoroughly research its causes and possible interventions, and take an intervention that seems likely to prevent after lots of thought (adapting as new evidence comes up). I’ll show that this recipe isn’t robust to unawareness.
Why? Because we lack both the following conditions for an intervention to be net-positive. (The examples come from the “Severe unawareness in AI safety” vignette.)
- Outcome robustness: Intervening on in a given direction would be net-positive.
- Example of failure: It’s unclear whether “human” space colonization (SC) is better than misaligned AI SC, given how many systematic ways these coarse categories could differ in various directions. (Especially when we consider exotic possibilities, like interactions with alien civilizations and acausal trade.)
- Implementation robustness: Our intervention on would (i) change in the intended direction, and (ii) avoid changing other variables in directions that might outweigh the intended positive effect.
- Example of failure: AI safety interventions might (i) increase the risk of human disempowerment by AI, e.g., by increasing AI companies’ complacency; or (ii) increase the risk of extinction by causes other than successful AI takeover, e.g., a great power war with novel WMDs.
Fig. 5 visually summarizes this distinction. As we’ll see in the rest of the sequence, it can be easy to mistakenly conclude an intervention is robust merely because it’s outcome-robust, neglecting implementation robustness (or vice versa).
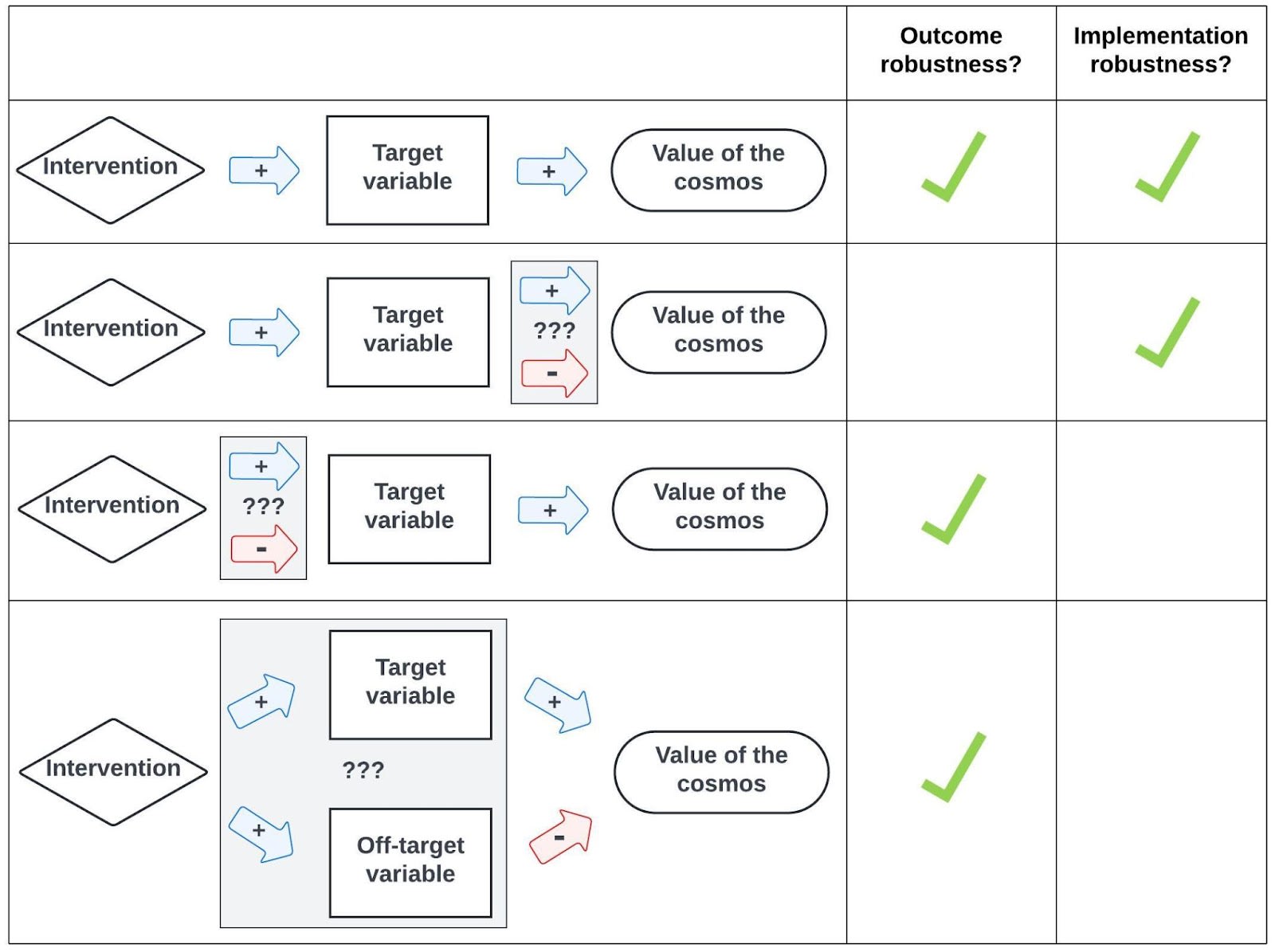 |
| Figure 5. A blue (resp. red) arrow from X to Y indicates that X increases (resp. decreases) Y. Informally, if we know how the value of the cosmos varies with some target variable, and we can adjust that variable (and only that variable)[6] as intended, our intervention is robustly better than inaction (row 1). But we could be unaware of effects of our target variable on total value (row 2); effects of our intervention on the target variable (row 3); or the presence of off-target variables affected by our intervention (row 4). |
The problem in detail
Key takeaway
When we model the impact of the AI safety intervention from the vignette, the structural problems above undermine the case for that intervention. That is, given reasonable ranges of parameter estimates, the intervention is positive under some estimates and negative under others, and it’s arbitrary how we weigh up their plausibility.
As in the vignette, let’s take “work on AI control” as our candidate intervention. We’ll model the value of the future as a function of different locked-in trajectories this intervention could lead to (cf. Greaves and MacAskill (2021, Sec. 4); Tarsney (2023)). Then we’ll imprecisely estimate this model’s parameters, and see whether the intervention is better than inaction.[7]
Suppose there are a few major categories of future trajectories that could get locked in soon, called attractor states. We might therefore expect our intervention’s UEV to be dominated by its impact on these lock-in events. Thus, in this model, our intervention doesn’t appreciably change the value of the future conditional on a given attractor state. We’ll use the following breakdown of hypotheses, corresponding to attractor states:
- Rogue: Earth-originating civilization locks in the values of human-disempowering AIs, then starts colonizing space.
- Benevolent: Earth-originating civilization locks in the values of relatively “benevolent” humans, then starts colonizing space.
- Malevolent: Earth-originating civilization locks in the values of relatively “malevolent” humans, then starts colonizing space.
- Other: Every other possibility (i.e., the catch-all).
Caveats:
- If we wanted, we could break down Other further into “Earth-originating civilization starts colonizing space before value lock-in”, “Earth-originating civilization is destroyed, but intelligent life re-evolves”, etc., and only then resort to a catch-all. Since this model is meant to be illustrative rather than super rigorous, I’ll group these scenarios together for the sake of tractability. I welcome arguments that a more fine-grained model would allow for strategy comparisons after all.
- Recall that in our model of UEV, we have imprecise credences over fine-grainings of hypotheses. (That’s what the “Example scenarios” in Table 1 correspond to.) I’ll make the simplifying assumption that the fine-grainings of the attractor states are independent from each other. This way, we get the set of UEVs the naïve way: Take the EV for each pair of (i) a distribution (from a set ) over the attractor states, and (ii) a list of values (from a list of ranges of values) for each attractor state .
- The exact numbers below are pulled out of thin air. That’s the point! What matters is that we don’t have reason to pin down value estimates (or credences) that are more precise than these ranges. If the objection is “these imprecise representations are arbitrary”, why would we answer this with “thus we should make a more arbitrary guess”?
Now, for any hypothesis out of the four above, let For any in our set of distributions , then, the value of working on AI control is:
Let’s assume is some “typical longtermist EA” value function. (The conclusion doesn’t hinge on this. What matters is that is impartial.) To define our units of value, let’s fix. Then, we have our imprecise estimates in Table 1, which we’ll plug into the equation above to see whether the intervention is net-positive.
Table 1. Ranges of wild guesses for factors in a model of the impact of AI control. All the quotes come from the vignette.
Factor[8] | Definition | Estimate | Brief reasoning |
| How our intervention changes p(rogue AI value lock-in and space colonization) | [-0.02, 0.01] | “The intended effects of AI control sure seem good. And maybe there are flow-through benefits, like inspiring others to work on AI safety too. But have I precisely accounted for the most significant ways that this research could accelerate capabilities, or AI companies that implement control measures could get complacent about misalignment, or the others I inspire to switch to control would’ve more effectively reduced AI risk some other way, or …?” | |
| How our intervention changes p(benevolent human value lock-in and space colonization) | [-0.005, 0.01] | Conditional on an intervention preventing (resp. causing) human disempowerment by AI, it seems plausible that the default alternative outcome is (resp. would have been) benevolent human lock-in. | |
| How our intervention changes p(every other possibility) | [-0.021, 0.026] | “Even if I reduce disempowerment risk, how do I weigh this against the possible effects on the likelihood of catastrophes that prevent SC entirely? For all I know, my biggest impact is on AI race dynamics that lead to a war involving novel WMDs.” | |
| Value of the future given rogue AI value lock-in and space colonization | [0, 1] | By definition. Example scenarios:
| |
| Value of the future given benevolent human value lock-in and space colonization | [0.2, 2] | “Maybe humans would differ a lot from AIs in how much (and what kind of) reflection they do before value lock-in, or how they approach philosophy, or how cooperative they are. Is our species unusually philosophically stubborn?” Example scenarios:
| |
| Value of the future given malevolent human value lock-in and space colonization | [-0.5, 0.1] | “And some human motivations are pretty scary, especially compared to what I imagine Claude 5.8 or OpenAI o6 would be like.” Example scenarios:
| |
| Value of the future given other possible trajectories | [-0.2, 1.5] | “And if no one from Earth colonizes space, how much better or worse might SC by alien civilizations be?” Example scenarios:
|
At last, we can see how the sign of an AI safety intervention varies across these plausible estimates (Table 2). I consider three pairs of parameter combinations consistent with these ranges. Each pair illustrates success vs. failure of robustness in the following ways:
- Rows 1-2 (outcome robustness): Is Benevolent better or worse than Rogue?
- Rows 3-4 (implementation robustness, type (i)): Do we decrease or increase the probability of Rogue?
- Rows 5-6 (implementation robustness, type (ii)): Holding fixed our impact on Rogue, do we only increase the probability of Benevolent, or do we also increase the probability of Other?
Table 2. Net effect of AI control on total value given three pairs of parameter combinations. Changes between subsequent rows in each pair are in bold.
| -0.020 | 0.0100 | 0.0090 | 0.7 | 2.0 | -0.2 | 0.0 | +0.0058 |
| -0.020 | 0.0100 | 0.0090 | 0.7 | 0.2 | -0.2 | 0.0 | -0.0122 |
| -0.005 | 0.0100 | -0.0100 | 0.0 | 0.6 | -0.1 | 0.5 | +0.0005 |
| 0.005 | 0.0100 | -0.0200 | 0.0 | 0.6 | -0.1 | 0.5 | -0.0045 |
| -0.002 | 0.0020 | 0.0000 | 0.1 | 0.6 | -0.5 | -0.2 | +0.0010 |
| -0.002 | 0.0004 | 0.0016 | 0.1 | 0.6 | -0.5 | -0.2 | -0.0003 |
It might be tempting to try averaging over these estimates (either with our intuitions or with equal weights), or to pick the story that seems most intuitively plausible. But as you’ll recall, moves like that don’t honestly represent our epistemic state.
 |
Concluding remarks. The imprecision of our estimates of strategies’ impact under unawareness, therefore, isn’t a mere technicality. There are deep and pervasive limitations on how much we can reasonably narrow down these estimates, which undermine action guidance from impartial altruism. By acknowledging these limitations, we have a more rigorous argument for my earlier conjecture: Attempting to prevent an “obviously bad” event isn’t, all things considered, better than nothing from an impartial perspective.
Despite this case for suspending judgment, perhaps existing frameworks from the EA canon let us compare strategies’ impartial impact? I’ll take up this question in the final post.
Appendix B: Formalism for unawareness-inclusive expected value
Let be a set of hypotheses in the awareness set that partitions the awareness set (i.e., these hypotheses cover all the possible worlds covered by the awareness set, and they’re mutually exclusive from each other).
- For each hypothesis in plus the catch-all , we (implicitly) have some set of “token” worlds. These are possible worlds contained in , which we’re not actually aware of, that represent the fine-grainings of we vaguely conceive of.
- In the example above, the set of sub-hypotheses corresponds to for the hypothesis “misaligned ASI takes over”.
- Our value function is now defined over every world in for every .
- Let be some set of probability distributions over the set of in , such that our (imprecise) credence in given strategy is .
- Note: Nothing in my argument turns on whether our credence in each is imprecise. We might have precise credences over hypotheses, yet imprecise credences over the fine-grainings within each hypothesis.
- Then, letting , the UEV of strategy is
Appendix C: Incomparability and “positive” interventions
Our definition of “better” under unawareness was: Strategy is better than if and only if has higher under all of our probability distributions in . Under this definition, then, “ is not better than ” does not imply “ is worse than, or exactly as good as, ”, since they could instead be incomparable. This has some implications that can be counterintuitive when we’re used to thinking we can always compare strategies.
Let denote some “default” or “do nothing” strategy. This might correspond to, e.g., living the life you’d prefer if you didn’t consider impartial consequentialism action-guiding at all, or not “intervening” on some global problem. We’ll say that is (robustly) positive if and only if is better than .
Positive interventions aren’t necessarily preferable to non-positive interventions. Suppose:
- is better than , but
- is incomparable with both and .
Then, you shouldn’t do , since it’s dominated by . But you don’t have a reason to choose over , even though is robustly positive while isn’t!
This might seem strange, since in discussions about cause robustness, we often tend to talk as if the goal is to find robustly positive interventions. But when incomparability is on the table, whether one action is “robustly positive” doesn’t necessarily indicate whether that action has better consequences, impartially speaking, than alternatives that aren’t positive. (Cf. St. Jules, section “Questions and possible implications”.)
Here’s a key implication of this observation. Suppose that if you currently do nothing, your future self might take some action at “crunch time” that is neither robustly positive nor negative (from their epistemic perspective). Whereas, if you instead think more about how to have a robustly positive impact (see “low-footprint Capacity-Building” in the final post), your future self will take an action that’s robustly positive — but not robustly better than the default action. Then with respect to UEV, you don’t have a reason to think more rather than do nothing. This is even assuming that you don’t value drift, and that thinking more doesn’t incur backfire risks between now and crunch time. Of course, this is an oversimplified picture, and perhaps there’s some non-UEV-based principle that could justify this kind of thinking more.
Preventing someone from doing a non-positive intervention can make your intervention non-positive. (Cf. St. Jules, section “Disfavours changing plans”.) The intuition here is: An intervention that isn’t robustly positive can nonetheless be highly positive with respect to some precisification of our beliefs, i.e., some in . So, if under we prevent someone else from implementing that intervention, this downside could be large enough to outweigh the upsides under .
Spelling this out, let be the set of probability distributions representing your beliefs. Suppose:
- There’s another decision-maker, Bob, who shares your value function but who has different beliefs, and (assume for the sake of simplicity) you can’t coordinate with him.
- If you do , Bob’s strategy will certainly be , and if you do , Bob’s strategy will certainly be .
- Both and are incomparable with (with respect to your beliefs ).
- Abusing notation to let denote an element of the UEV of Bob following strategy , we have .
So, represents how much value is lost via the influence of your intervention on Bob’s strategy, under . Then, if is sufficiently large, such that it outweighs the value gained via the influence of your intervention on other variables, overall we have . This implies isn’t positive, even though the mechanism by which backfires is that you prevent Bob from doing a non-positive intervention.
References
Greaves, Hilary, and William MacAskill. 2021. “The Case for Strong Longtermism.” Global Priorities Institute Working Paper No. 5-2021, University of Oxford.
Monton, Bradley. 2019. “How to Avoid Maximizing Expected Utility.” Philosophers’ Imprint 19.
Tarsney, Christian. 2023. “The Epistemic Challenge to Longtermism.” Synthese 201 (6): 1–37.
- ^
Many thanks to Violet Hour for suggesting the step-by-step structure of this section.
- ^
Technically, since the hypotheses we’re aware of can overlap, we should only iterate over some set of mutually exclusive hypotheses covering all the hypotheses we’re aware of, to avoid double-counting.
- ^
Let’s grant that we should aggregate the UEV interval, if we’re justified in pinning down a particular interval. Well, are we? As discussed above, the precise values for the fine-grainings are arbitrary approximations of possible worlds we’re not aware of. This means our underlying evaluation of some strategy, which UEV is intended to formalize, is too vague for us to non-arbitrarily pin down an aggregated UEV, either (see Clifton, section “Cluelessness”).
- ^
E.g., if you would’ve endorsed small-probability discounting (Monton 2019) when computing regular EV, you might endorse an unawareness-inclusive version of EV with small-probability discounting.
- ^
H/t Anni Leskelä.
- ^
To be clear, this part isn’t necessary for the intervention to be net-positive under unawareness. We could instead have reason to think the off-target effects are net-positive, or that the on-target benefits outweigh any off-target downsides.
- ^
I’m not privileging inaction here. The question is whether we have any reason to do the intervention rather than not do it.
- ^
Δp(Malevolent) is determined by the other Δp(X) factors.
