I think reducing x-risk is by far the most cost-effective thing we can do, and in an adequate world all our efforts would be flowing into preventing x-risk.
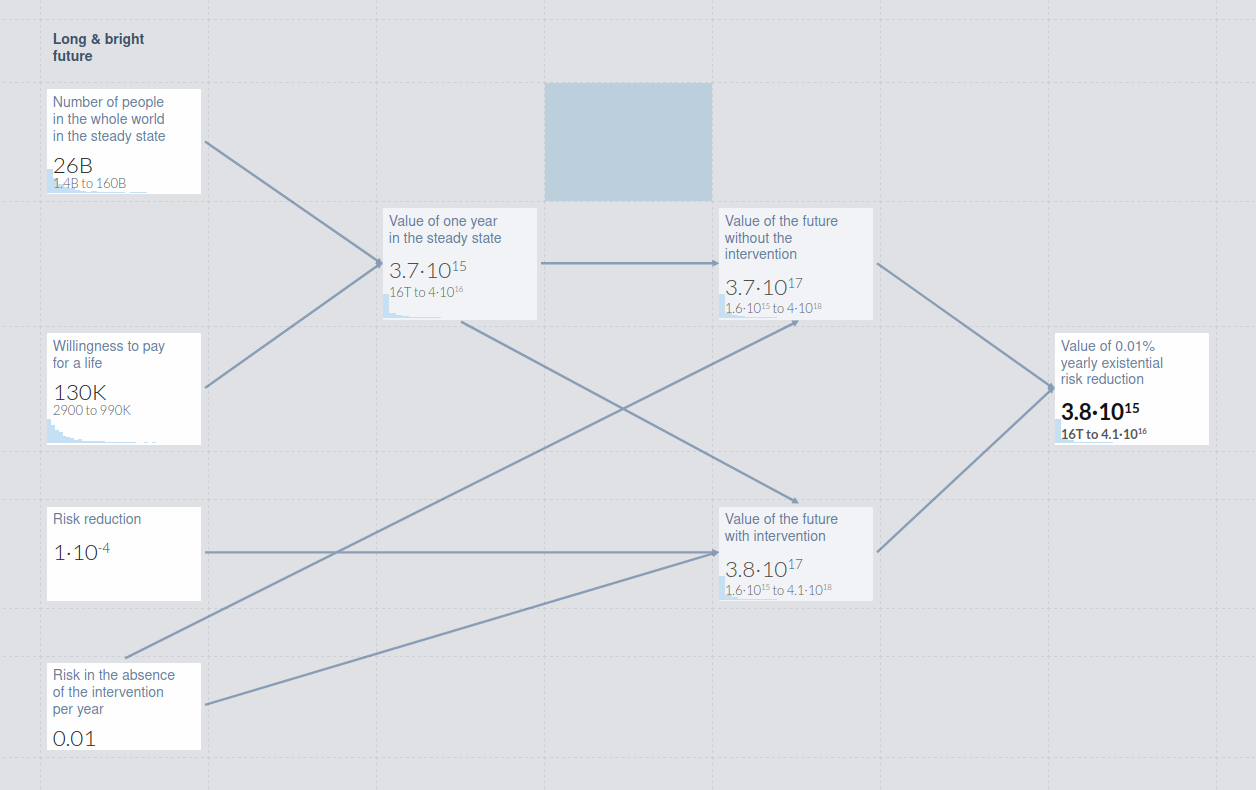
The utility of 0.01% x-risk reduction is many magnitudes greater than the global GDP, and even if you don't care at all about future people, you should still be willing to pay a lot more than currently is paid for 0.01% x-risk reduction, as Korthon's answer suggests.
But of course, we should not be willing to trade so much money for that x-risk reduction, because we can invest the money more efficiently to reduce x-risk even more.
So when we make the quite reasonable assumption that reducing x-risk is much more effective than doing anything else, the amount of money we should be willing to trade should only depend on how much x-risk we could otherwise reduce through spending that amount of money.
To find the answer to that, I think it is easier to consider the following question:
How much more likely is an x-risk event in the next 100 years if EA looses X dollars?
When you find the X that causes a difference in x-risk of 0.01%, the X is obviously the answer to the original question.
I only consider x-risk events in the next 100 years, because I think it is extremely hard to estimate how likely x-risk more than 100 years into the future is.
Consider (for simplicity) that EA currently has 50B$.
Now answer the following questions:
How much more likely is an x-risk event in the next 100 years if EA looses 50B$?
How much more likely is an x-risk event in the next 100 years if EA looses 0$?
How much more likely is an x-risk event in the next 100 years if EA looses 20B$?
How much more likely is an x-risk event in the next 100 years if EA looses 10B$?
How much more likely is an x-risk event in the next 100 years if EA looses 5B$?
How much more likely is an x-risk event in the next 100 years if EA looses 2B$?
Consider answering those questions for yourself before scrolling down and looking at my estimated answers for those questions, which may be quite wrong. Would be interesting if you also comment your estimates.
The x-risk from EA loosing 0$ to 2B$ should increase approximately linearly, so if x is the x-risk if EA looses 0$ and y is the x-risk if EA looses 2B$, you should be willing to pay d=0,01%y−x2B$ for a 0.01% x-risk reduction.
(Long sidenote: I think that if EA looses money right now, it does not significantly affect the likelihood of x-risk more than 100 years from now. So if you want to get your answer for the "real" x-risk reduction, and you estimate a z% chance of an x-risk event that happens strictly after 100 years, you should multiply your answer by 1/(1−z%) to get the amount of money you would be willing to spend for real x-risk reduction. However, I think it may even make more sense to talk about x-risk as the risk of an x-risk event that happens in the reasonably soon future (i.e. 100-5000 years), instead of thinking about the extremely long-term x-risk, because there may be a lot we cannot foresee yet and we cannot really influence that anyways, in my opinion.)
Ok, so here are my numbers to the questions above (in that order):
17%,10%,12%,10.8%,10.35%,10.13%
So I would pay 0.01%0.13%2B$=154M$ for a 0.01% x-risk reduction.
Note that I do think that there are even more effective ways to reduce x-risk, and in fact I suspect most things longtermist EA is currently funding have a higher expected x-risk reduction than 0.01% per 154M$. I just don't think that it is likely that the 50 billionth 2021 dollar EA spends has a much higher effectiveness than 0.01% per 154M$, so I think we should grant everything that has a higher expected effectiveness.
I hope we will be able to afford to spend many more future dollars to reduce x-risk by 0.01%.


I think one problem with your re-definition (that makes it imperfect IMO also) is apparent when thinking about the following questions: How likely is it that Earth-originating intelligent life eventually reaches >90% of its potential? How likely is it that it eventually reaches >0.1% of its potential? >0.0001% of its potential? >10^20 the total value of the conscious experiences of all humans with net-positive lives during the year 2020? My answers to these questions increase with each respective question, and my answer to the last question is several times higher than my answer to the first question.
Our cosmic potential is potentially extremely large, and there are many possible "very long-lasting, positive futures” (to use Holden's language from here) that seem "extremely good" from our limited perspective today (e.g. the futures we imagine when we read Bostrom's Letter from Utopia). But these futures potentially differ in value tremendously.
Okay, I just saw Zach's comment that he thinks value is roughly binary. I currently don't think I agree with him (see his first paragraph at that link, and my reply clarifying my view). Maybe my view is unusual?
Linch here:
I'd give similar answers for all 5 of those questions because I think most of the "existential catastrophes" (defined vaguely) involve wiping out >>99% of our potential (e.g. extinction this century before value/time increases substantially). But my independent impression is that there are a lot of "extremely good" outcomes in which we have a very long-lasting, positive future with value/year much, much greater than the value per year on Earth today, that also falls >99% short of our potential (and even >99.9999% of our potential).