Confidence: Medium, underlying data is patchy and relies on a good amount of guesswork, data work involved a fair amount of vibecoding.
Intro:
Tom Davidson has an excellent post explaining the compute bottleneck objection to the software-only intelligence explosion.[1] The rough idea is that AI research requires two inputs: cognitive labor and research compute. If these two inputs are gross complements, then even if there is recursive self-improvement in the amount of cognitive labor directed towards AI research, this process will fizzle as you get bottlenecked by the amount of research compute.
The compute bottleneck objection to the software-only intelligence explosion crucially relies on compute and cognitive labor being gross complements; however, this fact is not at all obvious. You might think compute and cognitive labor are gross substitutes because more labor can substitute for a higher quantity of experiments via more careful experimental design or selection of experiments. Or you might indeed think they are gross complements because eventually, ideas need to be tested out in compute-intensive, experimental verification.
Ideally, we could use empirical evidence to get some clarity on whether compute and cognitive labor are gross complements; however, the existing empirical evidence is weak. The main empirical estimate that is discussed in Tom's article is Oberfield and Raval (2014), which estimates the elasticity of substitution (the standard measure of whether goods are complements or substitutes) between capital and labor in manufacturing plants. It is not clear how well we can extrapolate from manufacturing to AI research.
In this article, we will try to remedy this by estimating the elasticity of substitution between research compute and cognitive labor in frontier AI firms.
Model
Baseline CES in Compute
To understand how we estimate the elasticity of substitution, it will be useful to set up a theoretical model of researching better algorithms. We will use a similar setup to Tom's article, although we will fill in the details.
Let denote an AI research firm and denote a time. Let denote the quality of the algorithms and denote the amount of inference compute used by research firm at time . We will let denote effective compute (Ho et al., 2024) for inference.
Algorithm quality improves according to the following equation:[2]
is the productivity scaling factor. denotes whether ideas, meaning proportional algorithmic improvements, get easier () or harder to find () as algorithmic quality increases, indexed by . maps research compute and cognitive labor to a value representing effective research effort. denotes a potential parallelization penalty.
We will assume is a constant returns to scale production function that exhibits constant elasticity of substitution, i.e.,
where is the elasticity of substitution between research compute and cognitive labor. denotes the case where compute and cognitive labor are gross substitutes, where they are gross complements, and denotes the intermediate, Cobb-Douglas case.
Conditions for a Software-Only Intelligence Explosion
Suppose that at time , an AI is invented that perfectly substitutes for human AI researchers. Further, suppose it costs compute to run that system. Then
denotes the number of copies that can be run.
We will be interested in whether an intelligence explosion occurs quickly after the invention of this AI. We will define an intelligence explosion as explosive growth in the quality of algorithms, . Explosive growth of implies at least explosive growth in the quantity of AIs.[3]
Since we are interested in what happens in the short-run, we will assume all variables except algorithmic quality remain fixed. That is, we study if a software-only intelligence explosion occurs.
By assumption, the AI can perfectly substitute for human AI researchers. Therefore, effective labor dedicated to AI research becomes
where denotes human labor.[4] Plugging this effective labor equation into the equation that defines changes in algorithm quality over time:
We can use this equation to study whether algorithm quality grows explosively. If the right hand side is a constant, then algorithm quality grows exponentially. But if the right hand side is an increasing function of , then algorithm quality experiences super-exponential growth, with an accelerating growth rate. For example, if where then growth is hyperbolic and reaches infinity in finite time.
The following are the necessary and sufficient conditions for explosive growth in :
To see why, let us go over the cases.
If , then the effective research effort term in our differential equation for is bounded. Intuitively, compute bottlenecks progress in effective research input. Therefore, the rate of growth of grows unboundedly if and only if the term grows over time i.e., .
If , then asymptotically we have
We get hyperbolic growth if and only if .
If , then we are in the same case as , except compute and cognitive labor are even more substitutable, so we drop the term.
The condition is exactly what Epoch and Forethought (see comments, Forethought actually considers the case) consider when they analyze whether the returns to research are high enough for a singularity.[5] They both find it possible that , although the evidence is imperfect and mixed across various contexts. Therefore, if , then a software-only intelligence explosion looks at least possible.
However, if , then a software-only intelligence explosion occurs only if . But if this condition held, we could get an intelligence explosion with constant, human-only research input. While not impossible, we find this condition fairly implausible.
Therefore, crucially affects the plausibility of a software-only intelligence explosion. If then it is plausible, but if it is not.
Deriving the Estimation Equation
We will estimate by looking at how AI firms allocate research compute and human labor from 2014 to 2024.
Of course, throughout this time period, the AI firms have been doing more than allocating merely research compute and human labor. Their activities included training AIs and serving AIs, in addition to the research-focused allocation of compute and human labor. Formally, they have been choosing a schedule of training compute , inference compute , research compute and human labor . However, we can split the firm's optimization problem into two parts:
- Dynamic Optimization: choosing where
- Static Optimization: choosing to minimize costs such that .
In this split, we have assumed that , i.e., that AIs did not contribute to cognitive labor before 2025.[6]
We will estimate using the static optimization problem. Let denote the cost of research compute and human labor respectively. Then the static optimization problem becomes
If we take the first-order conditions with respect to compute and cognitive labor, divide, take logs and re-arrange, we get the following equation:
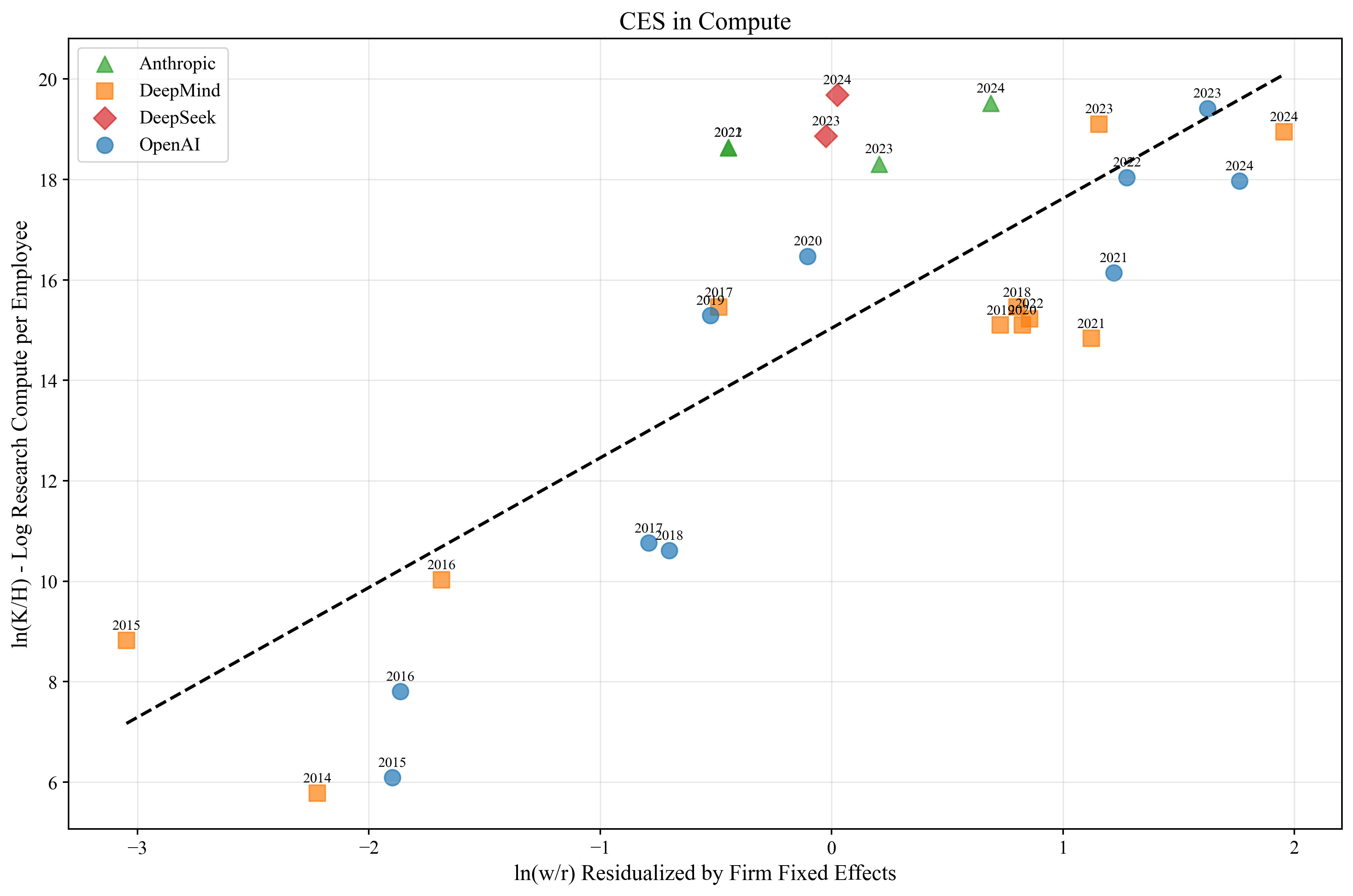
Therefore, we can estimate by regressing on a constant and and looking at the coefficient on . Intuitively, we can estimate how substitutable compute and labor are by seeing how the ratio of compute to labor changes as the relative price of labor to compute changes.
Alternative CES Formulation in Frontier Experiments
One potential problem with the baseline CES production function is that the required ratio of compute to labor in research does not depend on the frontier model size. Intuitively, as frontier models get larger, the compute demands of AI research should get larger as the firm needs to run near-frontier experiments. To accommodate this intuition, we will explore a re-parametrization of CES as an extension to our main, baseline results.
Let denote the number of near-frontier experiments a firm can run at time . is literally the number of frontier research training runs possible.[7] denotes the productivity benefit of extrapolating results from smaller experiments. For example, if you can accurately extrapolate experiments at of frontier compute then .[8] Now the change in algorithm quality over time is given by
We continue to suppose is CES. Following the same derivation steps as before, we get the following modified estimation equation:
We can estimate this equation by regressing on a constant, and . We will take the coefficient on as our estimate for .
Estimation
Data
To estimate the key equation described above, we need data on and . We attempt to gather this data for as many time periods and across as many major AI firms as we can. Unfortunately, this data is not always publicly available, so we do a good amount of guesswork. When we are guessing/extrapolating values, we try to note how uncertain we are. We incorporate these uncertainty estimates into our standard errors for the main results. If anyone knows any better data sources or can provide more accurate data here, we would be extremely interested.
Our data covers OpenAI from 2016-2024, Anthropic from 2022-2024, DeepMind from 2014-2024 and DeepSeek from 2023-2024. All prices are inflation-adjusted to 2023 USD. We use the following data sources.
We use headcount estimates from PitchBook which include headcount estimates at high frequency, roughly once per year. Unfortunately, the data does not make a distinction between research/engineering staff and operations/product staff. As long as the ratio of research to operations staff has been constant over time, our results will be unbiased.
: We first take estimates of from Epoch's notable models page, aggregating to the firm-year level by summing all training compute used across models in a given year. In cases where firms do not release (major) models in a given year, we assume training compute is the same as the prior year.
: The Information reported that the ratio of OpenAI's research to training compute spend was in 2024. Therefore, we multiply our estimate of by to get our estimate of . This is a significant limitation as we are assuming that the fraction of research to training compute is a constant across firms and times.[9] Out of all of our variables, this is the most coarse one.
: Our most reliable wage data comes from DeepMind and OpenAI's financial statements which include total spend on staff. Combined with our estimates of headcounts, we can recover average wages. DeepMind's financial statements cover 2014-2023, while OpenAI's statements cover its period as a nonprofit from 2016-2018. We fill in the rest of the years and firms using data from firms' job postings, Glassdoor, H1B Grader, levels.fyi, news sources, and BOSS Zhipin. We specifically look for and impute the wage of level III employees (scientific researchers) at each firm. We use salary instead of total compensation, assuming that salary is of total compensation.[10] While the financial statements data is reliable, the filled-in data has quite a bit of guesswork.
: We use the rental rate of GPUs according to Epoch's data. We match each AI firm with its cloud provider (e.g., OpenAI with Microsoft Azure) and use the corresponding rental rate. In reality, AI firms buy many GPUs, although in a competitive market the depreciated, present-discounted price should match the hourly rental rate.[11] We adjust for GPU quality by measuring the price in units of total FLOPs (e.g., FLOP/s times 3600 seconds in an hour) per dollar. We match firm-years to the GPUs that they were likely using at the time (e.g., OpenAI using A100s in 2022 and H100s in 2024). There is guesswork involved in the exact mix of GPUs that each firm is using in each year.
Trends
Before we get into estimation, we graph the following key variables. These are useful sanity checks, and if anyone has a good sense that these variables do not seem right, please let us know.
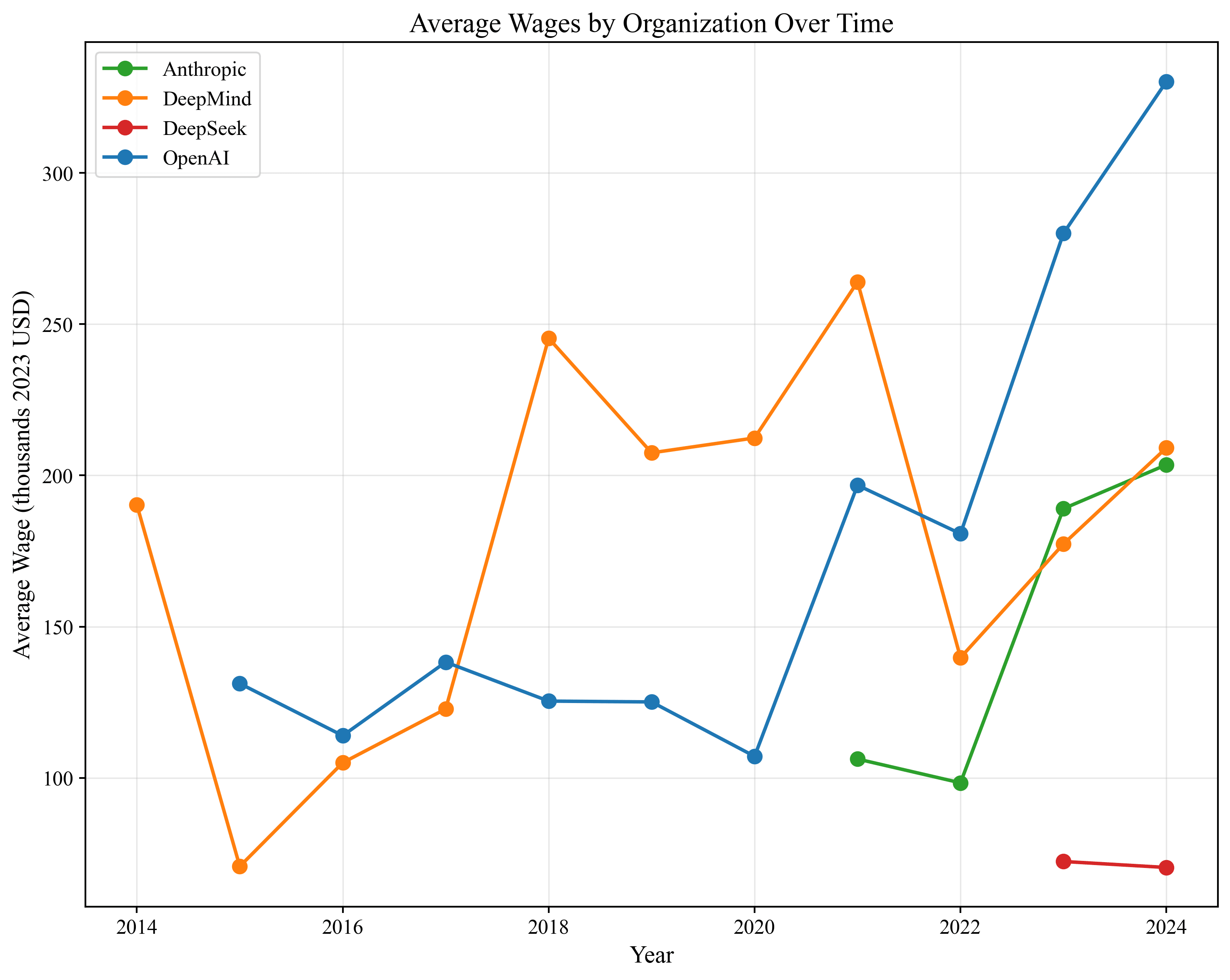
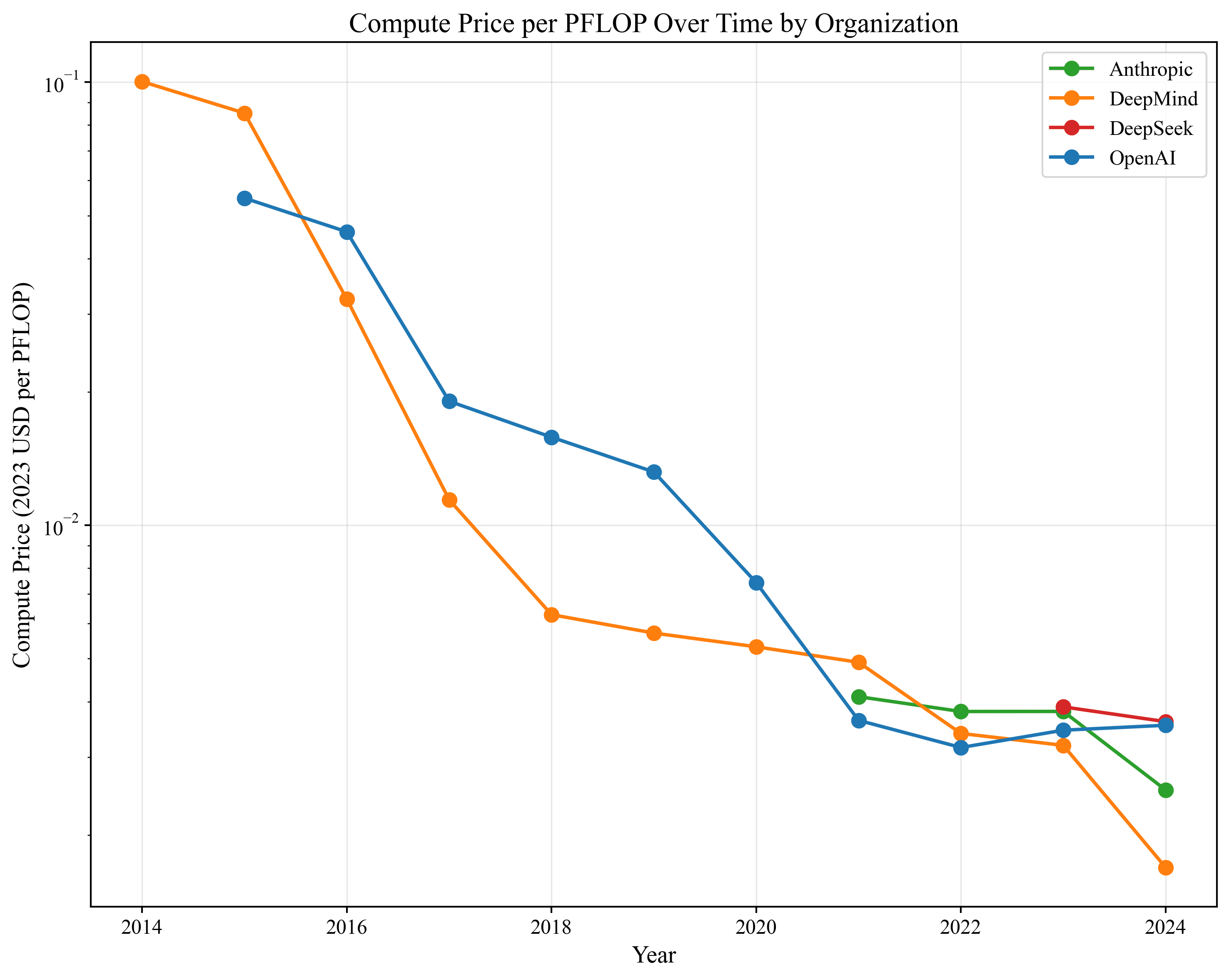
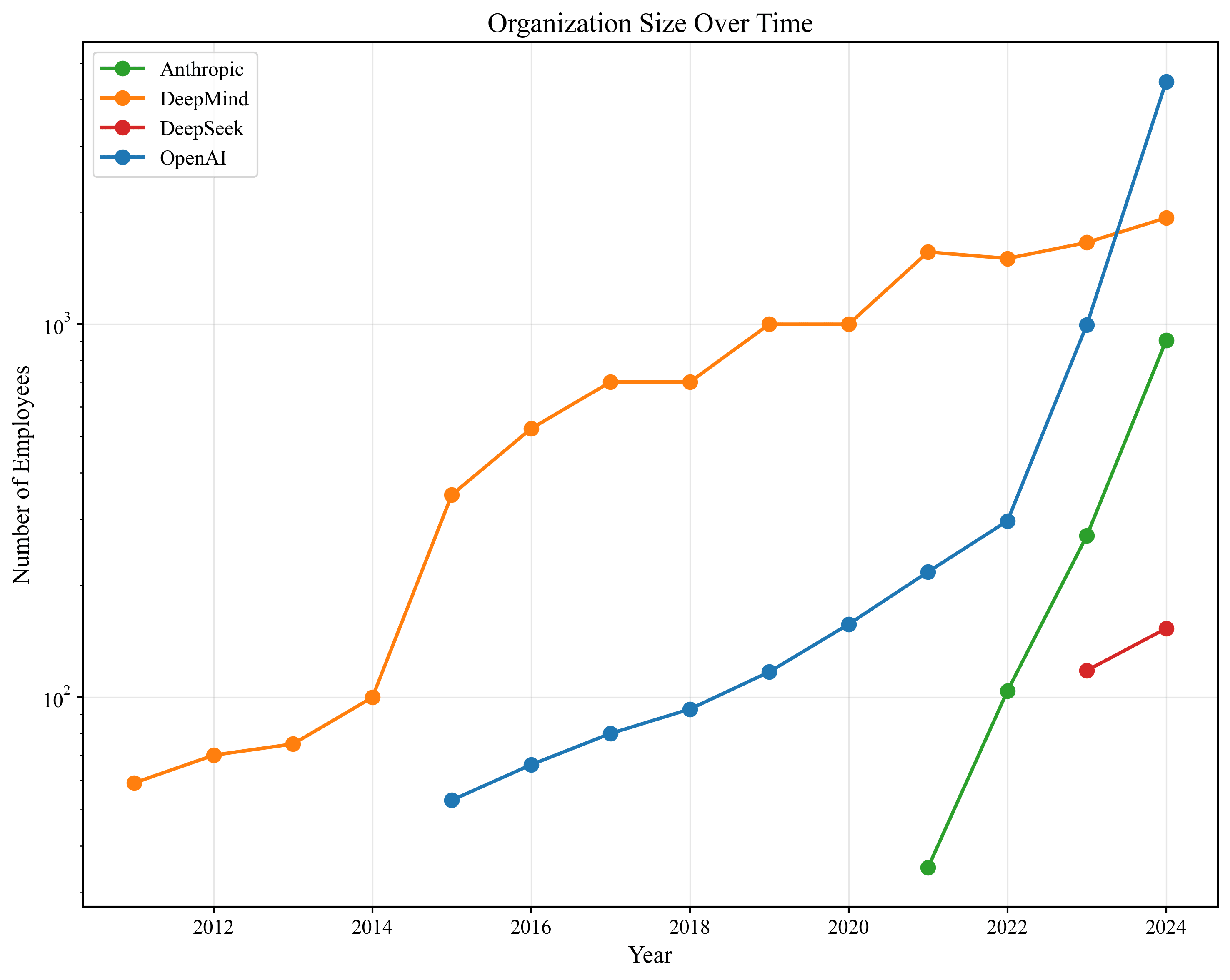
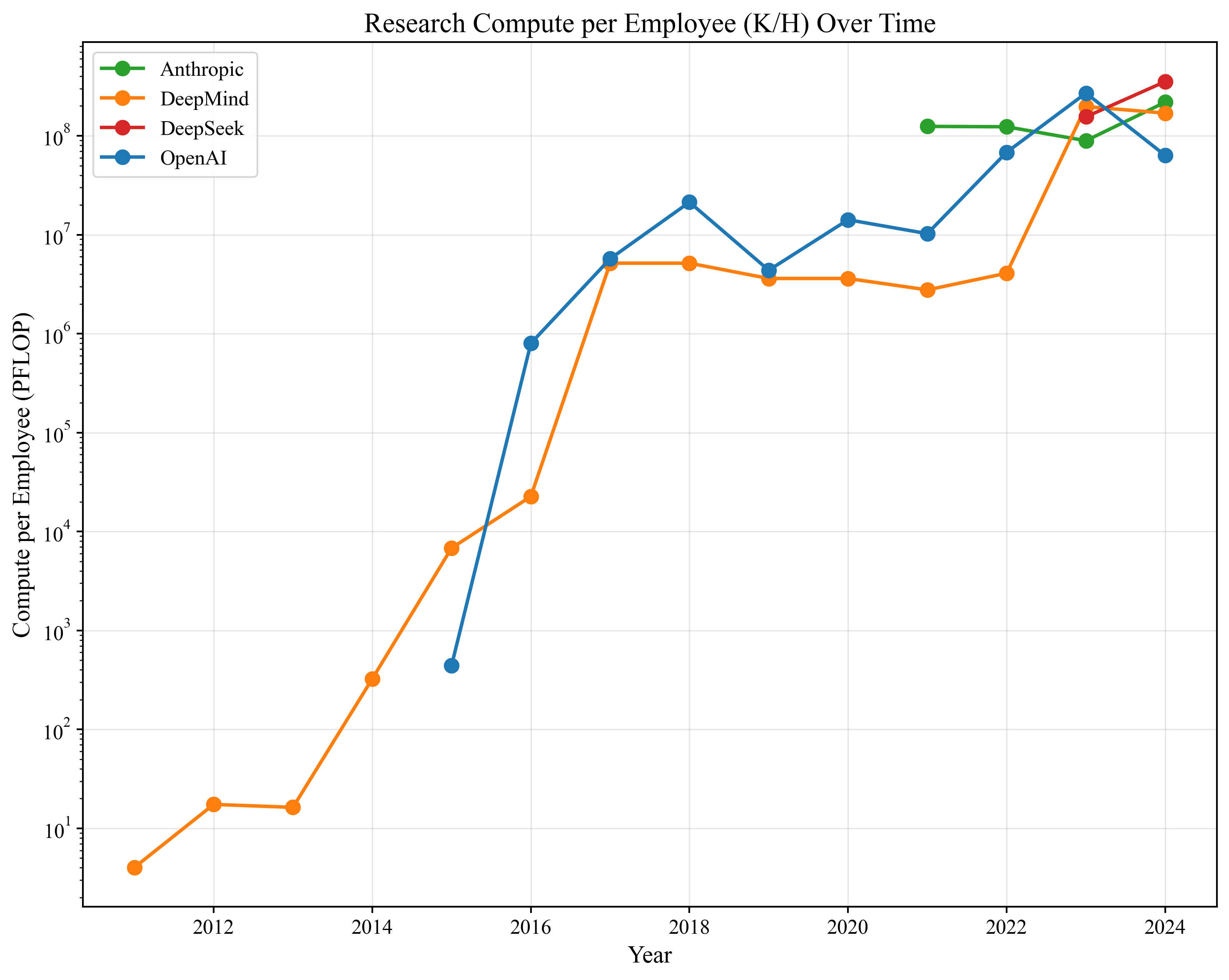
Estimation Results
We estimate two sets of main results, one for the CES in compute specification and one for CES in frontier experiments specification. For both sets of results, we include firm fixed effects to correct for any time-invariant productivity differences between firms.
| CES in Compute | CES in Frontier Experiments | |
| 2.58 | -0.10 | |
| SE | (.34) | (.18) |
| MCSE | [.68] | [0.30] |
Baseline standard errors (SE) are clustered at the firm level. We also run a Monte Carlo where we simulate independent noise in each variable according to our subjective uncertainty in the underlying data quality. Combining this Monte Carlo with a clustered bootstrap gives us our Monte Carlo standard errors (MCSE).
Our results show that how you model the situation matters quite a lot. In the CES in compute specification, we estimate , which implies research compute and cognitive labor are highly substitutable. However, in the frontier experiments case, we estimate . It is impossible in the economic model to have , although this estimate is well within the range of being 0 with some statistical error. In any case, this means that frontier experiments and labor are highly complementary. Recall would denote perfect complements, where increasing cognitive labor without a corresponding increase in near-frontier experiments would result in zero growth in algorithm quality.
To get a visual understanding of these fits, the following figure plots the regression result for the CES in compute specification. The slope of the fitted line corresponds to the estimated
The next figure corresponds to the regression result for CES in frontier experiments.
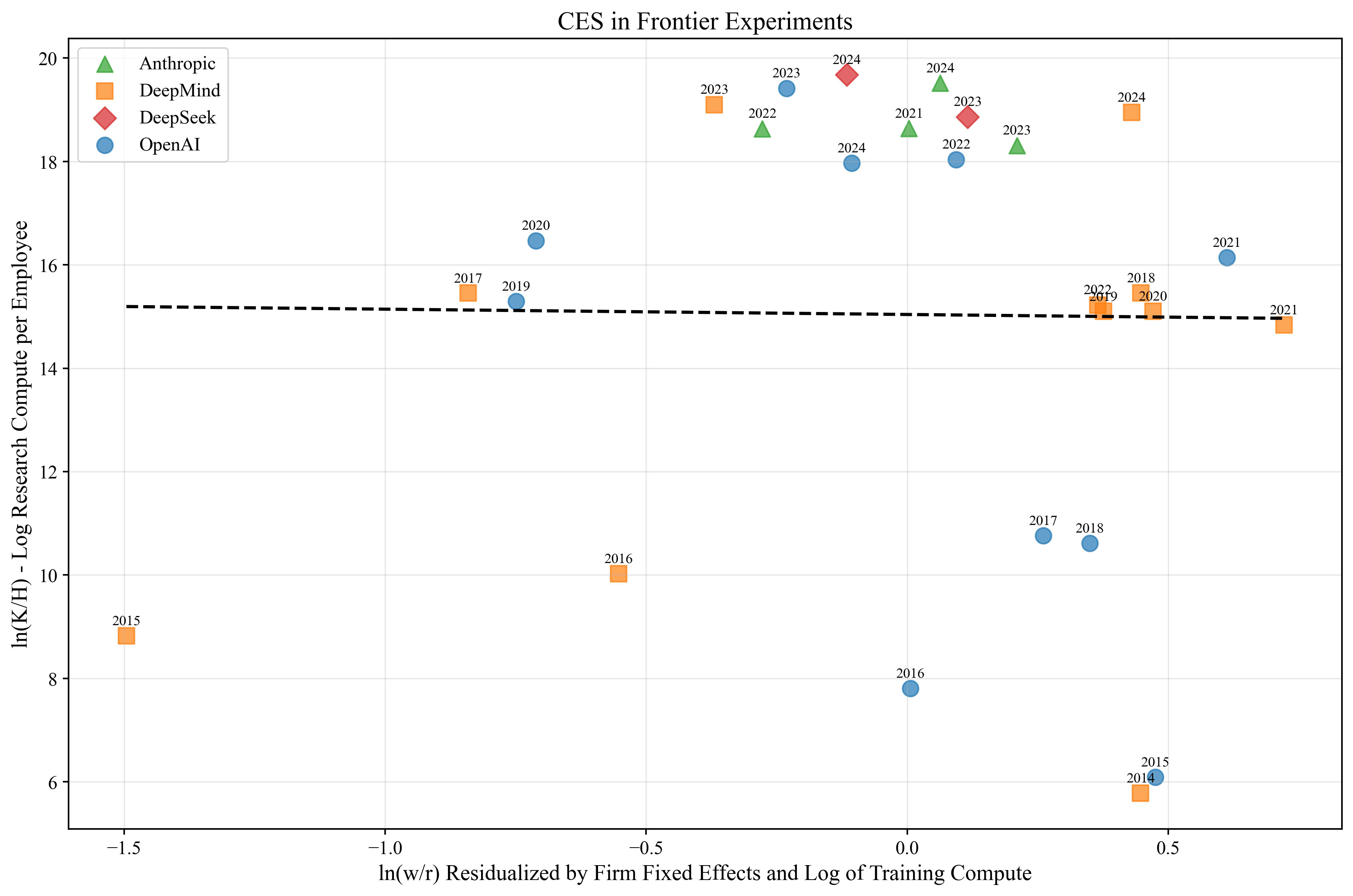
We also performed some basic robustness tests, like restricting the sample to after 2020 or 2022 (after GPT-3 or GPT-4 released), excluding 2024 (for the concern that AI had started to meaningfully assist in AI research), restricting the sample to DeepMind only (where we have the highest quality wage data), changing how we calculate wages, changing how we calculate research compute, etc. We get qualitatively similar results in all cases that we tried (substitutes in the CES in compute specification, complements in the CES in frontier experiments specification).
Results
The two different specifications give very different estimates of . If we had to choose between the specifications, we would choose the frontier experiments version. If the raw compute version was properly specified, then adding the training compute as a control should not change the coefficient on .[12] Therefore, our overall update from the evidence is that compute could majorly bottleneck the intelligence explosion.
But we do not update by a huge amount as this analysis has a lot of potential problems. It is not obvious which specification is correct, the underlying data has reliability problems and the data is from 4 firms across only a handful of years. On a more technical level, a large amount of variation is explained by firms scaling up training compute over time, there is endogeneity/simultaneity bias[13], and our analysis relies on simplifying assumptions such as the CES functional form and homogeneous, non-quality differentiated labor.
Thanks to Basil Halperin and Phil Trammell for reviewing the post and giving extensive comments.
- ^
The original version of this objection was made informally by Epoch researchers.
- ^
In reality, there is probably some algorithmic quality depreciation as you scale up training compute (e.g., algorithms that are good for GPT-2 might be bad for GPT-4). We could accommodate this intuition by adding a to the right-hand side of the equation for . But for our analysis, is fixed so this depreciation term would not matter.
- ^
If we additionally suppose that the intelligence of AI is an increasing, unbounded function of effective training compute, , then explosive growth of would also imply explosive growth in the intelligence of AIs. Of course, this assumes that the same algorithmic quality term affects inference compute and training compute.
- ^
As written, all inference compute is dedicated to AI research. We can easily weaken this assumption by having represent the compute cost divided by the fraction of inference compute dedicated to AI research. If we assume is constant over time, then we get the same equation.
- ^
There is a small notation difference as they denote the explosion condition as a fraction e.g., , while we express the condition as a sum e.g., .
- ^
We think this assumption is very defensible for 2023 and prior. 2024 is borderline, so we try excluding it from our analysis as a robustness check.
- ^
Note that algorithmic advances do not improve this ratio because they improve effective training compute and effective research compute at the same rate. Therefore, algorithmic advances simply cancel out.
- ^
To spell this out further, if research compute and training compute are equal, then by default you can run one experiment at the frontier. However, if you can extrapolate from experiments the size, then you can run 1000 experiments, so .
Further, the value of does not really matter. If is a fixed number (e.g., AIs are not better at extrapolating than humans), then does not change the conditions under which there is an intelligence explosion and it does not change the estimate of .
- ^
If this ratio has changed a lot over time, both of our estimates could be wrong. But in particular, the frontier experiments estimate could be badly wrong because we are essentially assuming that one of the inputs, number of frontier experiments, has been constant over time.
- ^
As long as the ratio of total compensation to salary has been constant over time, it does not matter which we use.
- ^
Note, however, the AI GPU market is not competitive, as Nvidia owns a huge fraction of the market. However, this Epoch paper finds that pricing calculation via ownership vs. rental rates are fairly similar.
- ^
This logic is far from airtight. If both models are misspecified, then adding a control can result in a more biased estimate.
- ^
We have a version of this analysis where we use local wages as an instrument to address potential endogeneity. We get similar results to the OLS version, but we omit them for brevity and because we are still thinking about better instruments.

I'm worried that trying to estimate σ by looking at wages is subject to lots of noise due to assumptions being violated, which could result in the large discrepancy you see between the two estimates.
One worry: I would guess that Anthropic could derive more output from extra researchers (1.5x/doubling?) than from extra GPUs (1.18x/doubling?), yet it spends more on compute than researchers. In particular I'd guess alpha/beta = 2.5, and wages/r_{research} is around 0.28 (maybe you have better data here). Under Cobb-Douglas and perfect competition these should be equal, but they're off by a factor of 9! I'm not totally sure but I think this would give you strange parameter values in CES as well. This huge gap between output elasticity and where firms are spending their money is strange to me, so I strongly suspect that one of the assumptions is broken rather than σ just being some extreme value like -0.10 or 2.58 with large firm fixed effects.
My guess at why: The AI industry is very different than it was in 2012 so it is plausible these firm fixed effects have actually greatly changed over time, which would affect the regression coefficients. Just some examples of possible changes over time:
Nevertheless I'm excited about the prospect of estimating σ and ϕ and I'm glad this was posted. Are you planning follow-up work, or is there other economic data we could theoretically collect that could give us higher confidence estimates?
Thanks for the insightful comment.
I take your overall point as the static optimization problem may not be properly specified. For example, costs may not be linear in labor size because of adjustment costs to growing very quickly or costs may not be linear in compute because of bulk discounting. Moreover, these non-linear costs may be changing over time (e.g., adjustment costs might only matter in 2021-2024 as OpenAI, Anthropic have been scaling labor aggressively). I agree that this would bias the estimate of σ. Given the data we have, there should be some way to at least partially deal with this (e.g., by adding lagged labor as a control). I'll have to think about it more.
On some of the smaller comments:
The best data we have is The Information's article that OpenAI spent $700M on salaries and $1000M on research compute in 2024, so the wLrK=.7 (assuming you meant wLrK instead of wr).
I agree. σ might not be constant over time, which is a problem for both estimation/extrapolation and also predicting what an intelligence explosion might look like. For example, if σ falls over time, then we may have a foom for a bit until σ falls below 1 and then fizzles. I've been thinking about writing something up about this.
Yes, although we're not decided yet on what is the most useful to follow-up on. Very short-term there is trying to accomodate non-linear pricing. Of course, data on what non-linear pricing looks like would be helpful e.g., how does Nvidia bulk discount.
We also may try to estimate ϕ with the data we have.
Thanks for this!
Let me try and summarise what I think is the high-level dynamic driving the result, and you can correct me if I'm confused.
CES in compute.
Compute has become cheaper while wages have stayed ~constant. The economic model then implies that:
Labs aren't doing this, suggesting that compute and labour are substitutes.
CES in frontier experiments.
Frontier experiments have become more expensive while wages have stayed ~constant. The economic model then implies that:
Labs are indeed doing this, suggesting that compute and labour are indeed complements.
(Though your 'Research compute per employee' data shows they're not doing that much since 2018, so the argument against the intelligence explosion is weaker here than I'd have expected.)
Yep, I think this gets the high-level dynamics driving the results right.
This argument neglects improvements in speed and capability right? Even if parallel labor and compute are complements, shouldn't we expect it is possible for increased speed or capabilities to substitute for compute? (It just isn't possible for AI companies to buy much of this.)
(I'm not claiming this is the biggest problem with this analysis, just noting that it is a problem.)
Yep. We are treating L as homogenous (no differentiation in skill, speed, etc.) I'm interested in thinking about quality differentiation a bit more.
Hmm, I think a software-only intelligence explosion is plausible even if σ<1, but without the implication that you can do it with human-only research input.
The basic idea is that when you double the efficiency of software, you can now:
So both the inputs to software R&D double.
I think this corresponds to:
dA = A^phi F(A K_res, A K_inf)
And then you only need phi > 0 to get an intelligence explosion. Not phi > 1.
This is really an explosion in the efficiency at which you can run AI algorithms, but you could do that for a while and then quickly use your massive workforce to develop superintelligence, or start training your ultra-efficient algorithms using way more compute.
hmm, I think I would expect different experience curves for the efficiency of running experiments vs producing cognitive labour (with generally less efficiency-boosts with time for running experiments). Is there any reason to expect them to behave similarly?
(Though I think I agree with the qualitative point that you could get a software-only intelligence explosion even if you can't do this with human-only research input, which was maybe your main point.)
Agree that i wouldn't particularly expect the efficiency curves to be the same.
But if the phi>0 for both types of efficiency, then I think this argument will still go through.
To put it in math, there would be two types of AI software technology, one for experimental efficiency and one for cognitive labour efficiency: A_exp and A_cog. The equations are then:
dA_exp = A_exp^phi_exp F(A_exp K_res, A_cog K_inf)
dA_cog = A_cog^phi_cog F(A_exp K_res, A_cog K_inf)
And then I think you'll find that, even with sigma < 1, it explodes when phi_exp>0 and phi_cog>0.
I spent a bit of time thinking about this today.
Lets adopt the notation in your comment and suppose that F(⋅) is the same across research sectors, with common λ. Let's also suppose common σ<1.
Then we get blow up in Acog iff
{ϕcog+λ>1if ϕcog≤ϕexpmax{ϕcog,ϕexp+λ}>1if ϕcog>ϕexp
The intution for this result is that when σ<1, you are bottlenecked by your slower growing sector.
If the slower growing sector is cognitive labor, then asympotically F∝Acog, and we get ˙A∝AϕcogcogAλcog so we have blow-up iff ϕcog+λ>1.
If the slower growing sector is experimental compute, then there are two cases. If experimental compute is blowing up on its own, then so is cogntive labor because by assumption cognitive labor is growing faster. If experimental compute is not blowing up on its own then asympotically F∝Aexp and we get ˙Acog∝AϕcogcogAλexp. Here we get a blow-up iff ϕcog>1.[1]
In contrast, if σ>1 then F is approximately the fastest growing sector. You get blow-up in both sectors if either sector blows up. Therefore, you get blow-up iff max{ϕcog+λ,ϕexp+λ}>1.
So if you accept this framing, complements vs substitutes only matters if some sectors are blowing up but not others. If all sectors have the returns to research high enough, then we get an intelligence explosion no matter what. This is an update for me, thanks!
I'm only analyzing blow-up conditions here. You could get e.g. double exponential growth here by having ϕcog=1 and ϕexp+λ=1.
Nice!
I think that condition is equivalent to saying that A_cog explodes iff either
Where the second possibility is the unrealistic one where it could explode with just human input
If your algorithms get more efficient over time at both small and large scales, and experiments test incremental improvements to architecture or data, then they should get cheaper to run proportionally to algorithmic efficiency of cognitive labor. I think this is better as a first approximation than assuming they're constant, and might hold in practice especially when you can target small-scale algorithmic improvements.
OK I see the model there.
I guess it's not clear to me if that should hold if I think that most experiment compute will be ~training, and most cognitive labour compute will be ~inference?
However, over time maybe more experiment compute will be ~inference, as it shifts more to being about producing data rather than testing architectures? That could push back towards this being a reasonable assumption. (Definitely don't feel like I have a clear picture of the dynamics here, though.)
This is a good point, we agree, thanks! Note that you need to assume that the algorithmic progress that gives you more effective inference compute is the same that gives you more effective research compute. This seems pretty reasonable but worth a discussion.
Although note that this argument works only with the CES in compute formulation. For the CES in frontier experiments, you would have the AKresAKtrain so the A cancels out.[1]
You might be able to avoid this by adding the A's in a less naive fashion. You don't have to train larger models if you don't want to. So perhaps you can freeze the frontier, and then you getAKresAfrozenKtrain? I need to think more about this point.
Yep, as you say in your footnote, you can choose to freeze the frontier, so you train models of a fixed capability using less and less compute (at least for a while).
Also, updating this would change all the intelligence explosion conditions, not just when σ<1.
Note that if you accept this, our estimation of σ in the raw compute specification is wrong.
The cost-minimization problem becomes
minH,KwH+rKs.t.F(AK,H)=¯F.
Taking FOCs and re-arranging,
KH=σγ1−γ+σlnwAr
So our previous estimation equation was missing an A on the relative prices. Intuitively, we understated the degree to which compute was getting cheaper. Now A is hard to observe, but let's just assume its growing exponentially with an 8 month doubling time per this Epoch paper.
Imputing this guess of A, and estimating via OLS with firm fixed effects gives us σ=.89 with .10standard errors.
Note that this doesn't change the estimation results for the frontier experiments since the A in AKresAKtrain just cancels out.
Though we initially consider this, we then adjust for compute as an input to R&D and so end up considering the sigma=1 condition. It's under that condition that I think it's more likely than not that the condition for a software-only intelligence explosion holds
Thanks for the clarification. We updated the post accordingly.
This is lovely, thank you!
My main concern would be that it takes the same very approximating stance as much other writing in the area, conflating all kinds of algorithmic progress into a single scalar 'quality of the algorithms'.
You do moderately well here, noting that the most direct interpretation of your model regards speed or runtime compute efficiency, yielding 'copies that can be run' as the immediate downstream consequence (and discussing in a footnote the relationship to 'intelligence'[1] and the distinction between 'inference' and training compute).
I worry that many readers don't track those (important!) distinctions and tend to conflate these concepts. For what it's worth, by distinguishing these concepts, I have come to the (tentative) conclusion that a speed/compute efficiency explosion is plausible (though not guaranteed), but an 'intelligence' explosion in software alone is less likely, except as a downstream effect of running faster (which might be nontrivial if pouring more effective compute into training and runtime yields meaningful gains).
Of course, 'intelligence' is also very many-dimensional! I think the most important factor in discussions like these regarding takeoff is 'sample efficiency', since that's quite generalisable and feeds into most downstream applications of more generic 'intelligence' resources. This is relevant to R&D because sample efficiency affects how quickly you can accrue research taste, which controls the stable level of your exploration quality. Domain-knowledge and taste are obviously less generalisable, and harder to get in silico alone. ↩︎
(comment originally posted on Twitter, Cheryl's response here)
I'll flag that estimating firm-level training compute with [Epoch AI's] notable models dataset will produce big underestimates. E.g. with your methodology, OpenAI spent ~4e25 FLOP on training and 1.3e25 FLOP on research in 2023 and 2024. the latter would cost ~$30 million. but we know OpenAI spent at least $1 billion on research in 2024! (also note they spent $1 billion on research compute after amortizing this cost with an undisclosed schedule).
But I don't have a great sense of how sensitive your results are to this issue.
(this raises other questions: what did OpenAI spend $3 billion in training compute on in 2024? that's enough for 50 GPT-4 sized models. Maybe my cost accounting is quite different from OpenAI's. A lot of that "training" compute might really be more experimental)
Here is a fleshed out version of Cheryl's response. Lets suppose actual research capital is qK but we just used K in our estimation equation.
Then the true estimation equation is
lnqKL=σlnγ1−γ+σlnwr
re-arranging we get
lnKL=σlnγ1−γ−lnq+σlnwr
So if we regress lnKL on a constant and lnwr then the coefficient on lnwr is still σ as long as q is independent of w/r.
Nevertheless, I think this should increase your uncertainty in our estimates because there is clearly a lot going on behind the scenes that we might not fully understand - like how is research vs. training compute measured, etc.
Thank you for this interesting post.
“By assumption, the AI can perfectly substitute for human AI researchers.”
Any idea/intuition about what would happen if you relaxed this assumption?
Without this assumption, recursive self improvement is a total non starter. RSI relies on an improved AI being able to design future AIs ("we want Claude N to build Claude N+1")
In complete generality, you could write effective labor as
L=Z(H,AKinf,AKtrain).
That is, effective labor is some function of the number of human researchers we have, the effective inference compute we have (quantity of AIs we can run) and the effective training compute (quality of AIs we trained).
The perfect substitution claim is that once training compute is sufficiently high, then eventually we can spend the inference compute on running some AI that substitutes for human researchers. Mathematically, for some x,
Z(H,AKinf,x)=H+AKinfc
where c is the compute cost to run the system.
So you could think of our analysis as saying, once we have an AI that perfectly substitutes for AI researchers, what happens next?
Now of course, you might expect substantial recursive self-improvement even with an AI system that doesn't perfectly substitute for AI labor. I think this is a super interesting and important question. I'm trying to think more about this question, but its hard to make progress because its unclear what Z(⋅) looks like. But let me try to gesture at a few things. Let's fix x at some sub-human level
If you assume say Cobb-Douglas, i.e.
Z(H,AKinf,x)=Hα(x)AKinfc1−a(x)
where 1−α(x) denotes the share of labor tasks that AI can do, then you'll pick up another 1−α(x) in the explosion condition i.e. ϕ+λ>1 will become ϕ+(1−α(x))λ>1. This captures the intuition that as the fraction of tasks an AI can do increases, the explosion condition gets easier and easier to hit.
Thanks for this Parker. I continue to think this research is insanely cool.
I agree with 1)
On 2), the condition you find makes sense, but aren't you implicitly assuming an elasticity of substitution of 1 with Cobb-Douglas?
Could be interesting to compare with Aghion et al. 2017. They look at a CES case with imperfect substitution (i.e., humans needed for some tasks).
https://www.nber.org/system/files/working_papers/w23928/w23928.pdf
Yes, definitely. In general, I don't have a great idea about what Z(⋅) looks like. The Cobb-Douglas case is just an example.
We are still working on getting a more official version of this on Arvix, possibly with estimates for λ and ϕ.
When we do that, we'll also upload full replication files. But I don't want to keep anyone waiting for the data in case they have some uses for it, so see here for the main CSV we used: https://github.com/parkerwhitfill/EOS_AI
Arxiv link here https://arxiv.org/abs/2507.23181