Hide table of contents

Comment Permalink

This is a neat tool!

Just a little heads up for people in terms of privacy. If you use the built-in helper to place your bets, your API key is sent to the owner of the manifolo service. I've glanced over the source code, and it does not seem to be stored anywhere. It's mainly routed through the backend for easier integration with an SDK and some logging purposes (as far as I can tell). However, there aren't really any strong guarantees that the source code publicly available is in fact the source code running on the URL.

I have no reason to doubt this, but in theory your API key might be stored and could be misused at a later date. For example, a holder of many API keys could place multiple bets quickly from many different users to steer a market or make a quick profit before anyone realizes.

I don't think there is any technical reason why the communication with the manifold APIs couldn't just happen on the frontend, so it might be worth looking into?

In general one should be very careful about pasting in API keys anywhere you don't trust. Seems like the key for manifold gives the holder very wide permissions on your account.

Again, I have no reason to suspect that there is anything sinister going on here, but I think it's worth pointing out nevertheless!

Thanks for posting the source code as well! Personally I did use my API key while testing and I do trust the author :)

Will Howard🔹

Good point, this is worth considering :) I tried to do this initially but it was blocked by Manifold's CORS policy. I was trying to keep everything in the frontend but this and the call to fetch the authenticated user both require going via a server unfortunately. Also something else to note in terms of privacy: I log the username and the amount when someone places a bet. It doesn't need the API key at all to calculate the recommended amount, so for people concerned about this you can just paste the amount into Manifold

Håkon Harnes 🔸2y2

Ah, yes, the CORS policy would be an obstacle. It might be possible to contact them and ask to be added to the list.

See in context

Manifolio: The tool for making Kelly optimal bets on Manifold Markets

by Will Howard🔹

Aug 10 20233 min read 20

82

ForecastingManifold MarketsPrediction markets

Frontpage

Manifolio: The tool for making Kelly optimal bets on Manifold Markets

Why bet Kelly (redux)?

For you

For the good of the epistemic environment

21 comments

This is a linkpost for https://manifol.io/

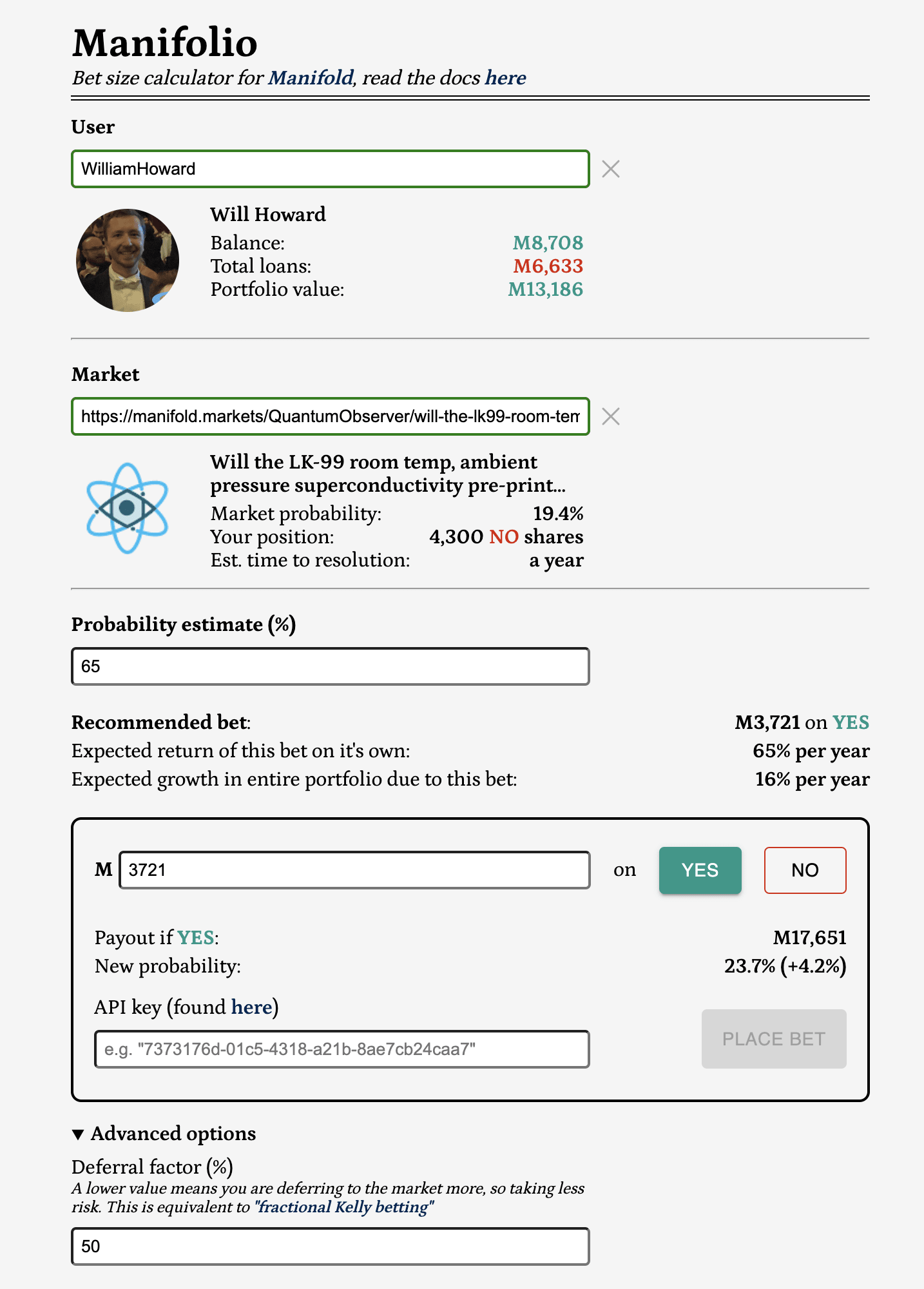
I've made a calculator that makes it easy to make correctly sized bets on Manifold. You just put in the market and your estimate of the true probability, and it tells you the right amount to bet according to the Kelly criterion.

“The right amount to bet according to the Kelly criterion” means maximising the expected logarithm of your wealth.

There is a simple formula for this in the case of bets with fixed odds, but this doesn’t work well on prediction markets in general because the market moves in response to your bet. Manifolio accounts for this, plus some other things like the risk from other bets in your portfolio. I've aimed to make it simple and robust so you can focus on estimating the probability and trust that you are betting the right amount based on this.

You can use it here (with a market prefilled as an example), or read a more detailed guide in the github readme. It's also available as a chrome extension... which currently has to be installed in a slightly roundabout way (instructions also in the readme). I'll update here when it's approved in the chrome web store.

EDIT: Good news! The extension has now been approved and can be installed from the web store.

Why bet Kelly (redux)?

Much ink has been spilled about why maximising the logarithm of your wealth is a good thing to do. I’ll just give a brief pitch for why it is probably the best strategy, both for you, and for “the good of the epistemic environment”.

For you

Given a specific wealth goal, it minimises the expected time to reach that goal compared to any other strategy.
It maximises wealth in the median (50th percentile) outcome.
Furthermore, for any particular percentile it gets arbitrarily close to being the best strategy as the number of bets gets very large. So if you are about to participate in 100 coin flip bets in a row, even if you know you are going to get the 90th percentile luckiest outcome, the optimal amount to bet is still close to the Kelly optimal amount (just marginally higher). In my opinion this is the most compelling self-interested reason, even if you get very lucky or unlucky it’s never far off the best strategy.

(the above are all in the limit of a large number of iterated bets)

There are also some horror stories of how people do when using a more intuition based approach... it's surprisingly easy to lose (fake) money even when you have favourable odds.

For the good of the epistemic environment

A marketplace consisting of Kelly bettors learns at the optimal rate, in the following sense:

Special property 1: the market will produce an equilibrium probability that is the wealth weighted average of each participant’s individual probability estimate. In other words it behaves as if the relative wealth of each participant is the prior on them being correct.
Special property 2: When the market resolves one way or the other, the relative wealth distribution ends up being updated in a perfectly Bayesian manner. When it comes time to bet on the next market, the new wealth distribution is the correctly updated prior on each participant being right, as if you had gone through and calculated Bayes’ rule for each of them.

Together these mean that, if everyone bets according to the Kelly criterion, then after many iterations the relative wealth of each participant ends up being the best possible indicator of their predictive ability. And the equilibrium probability of each market is the best possible estimate of the probability, given the track record of each participant. This is a pretty strong result^[1]!

...

I'd love to hear any feedback people have on this. You can leave a comment here or contact me by email.

Thanks to the people who funded this project on Manifund, and everyone who has given feedback and helped me test it out

^{^}
This is shown in this paper. Importantly it's proven for the case of one market at a time, not when there are multiple markets running concurrently. I’m reasonably confident a version of it is still true with concurrent markets, but in any case Manifolio doesn't currently account for the opportunity cost of not betting in other markets, so this result doesn't carry over exactly.

82 Reactions

More posts like this

111

Predictive Performance on Metaculus vs. Manifold Markets

nikos

The World in 2029

Nathan Young

144

Rational predictions often update predictably*

Gregory Lewis🔸

Comments20

Sorted by

New & upvoted

Click to highlight new comments since: Today at 10:33 AM

Matthew_Barnett2y12

This looks like it could be an excellent and helpful tool. I'll probably try using it to choose bet sizes at some point. I have a general critique though. I think it generally makes sense to treat your wealth as including a discounted sum of future income. For example, most young people have very little wealth on paper, and yet it is often highly rational for them to put substantial amounts of their money in the stock market, even though it's more risky than a savings account. The same is true for Manifold users. They can usually make lots of "income" by creating markets, completing quests, and purchasing mana directly. If you exclude these things from the calculation, I predict you'll often end up with an unreasonably low tolerance for risk.

Writer2y3

Easy fix: let the user pick a discounted sum of future income. It could also be calculated using some average over past daily income if that's available to see.

Simon Eckerström Liedholm3mo1

@Will Howard🔹 It seems like the web tool no longer works (I'm not able to use it at least) - it doesn't accept links to user profiles for example.

Jackson Wagner2y4

This is great; I've used it a few times over the past month and it's been interesting/helpful!

Here is a suggestion for a very similar tool: I would love to use some kind of "arbitrage calculator". If I think that two markets with different prices have substantially the same criteria (for example, these three markets, which were priced at 24%, 34%, and 53% before I stepped in), obviously I can try to arbitrage them! But there are many complications that I haven't been able to think through very clearly:

One market might be much smaller than the other, so betting 100 mana would push the probability much further in one market than the other. Do I arbitrage by betting equal amounts of mana in both markets, or betting to move the probabilities by equal amounts (surely not), or some intelligent mix of the two?
How should I bet if I spot an arbitrage opportunity where the criteria are (inevitably) ALMOST the same, but not exactly the same? Say the two prices are separated by 25 percentage points, but I think the difference in resolution criteria only justifies a 5 percentage point difference? (Or the same problem in reverse -- spotting two similarly-priced markets where I think there should be a larger difference between them.)
What if I am not just purely arbitraging, but also have a my own inside view about what the true probability should be? There must be some optimal way to make a semi-hedged bet that maximizes my profits! But I don't know enough about finance to begin to figure out what this might be...

If you added this capability to manifolio, I feel like I would use it all the time! Having an arbitrage calculator might help create more liquid markets in manifold, by helping unify markets on related topics and generate more consistent probabilities.

Håkon Harnes 🔸2y4

Will Howard🔹2y2

Good point, this is worth considering :)

I don't think there is any technical reason why the communication with the manifold APIs couldn't just happen on the frontend, so it might be worth looking into?

I tried to do this initially but it was blocked by Manifold's CORS policy. I was trying to keep everything in the frontend but this and the call to fetch the authenticated user both require going via a server unfortunately.

Also something else to note in terms of privacy: I log the username and the amount when someone places a bet.

It doesn't need the API key at all to calculate the recommended amount, so for people concerned about this you can just paste the amount into Manifold

Håkon Harnes 🔸2y2

Ah, yes, the CORS policy would be an obstacle. It might be possible to contact them and ask to be added to the list.

Austin2y4

Thanks for building this! Kelly criteria is one of those super neat concepts that has had a lot of analysis, but not much "here's a thing you can play with". I love that Manifolio lets you play with different users and markets, to give a more intuitive sense of what the Kelly Criteria means. The UI is simple and communicates key info quickly, and I like that there's a Chrome extension for tighter integration!

sam_brenner2y3

Maybe this is stupid of me, but should this be a fraction of your balance or a fraction of your net asset value?

sam_brenner2y3

I ask because of this message I got

"You have total loans greater than your current balance. Under strict Kelly betting, you should not bet at all in this scenario because there is non-zero risk of ruin. This calculator allows some leeway in this, and will still recommend a bet as long as losing all your money does not actually occur in any of the (up to 50,000) scenarios it simulates."

Does this take into account the fact that I could liquidate a position to generate more balance and avoid ruin?

Will Howard🔹2y3

It doesn't account for that unfortunately, one of the simplifying assumptions it makes is that you will wait for all your positions to resolve rather than selling them.

Will Howard🔹2y2

It directly calculates the amount that will maximise expected log wealth, rather than using a fixed fraction. Basically it simulates the possible outcomes of all the other bets you have open. Then it adds in the new bet you are making and adjusts the size to maximise expected log wealth once all the bets have resolved.

If you have a very diversified portfolio of other bets this will be almost the same as betting the Kelly fraction (the f = p - q/b version) of your net asset value. If you have a risker portfolio, such as one massive bet, then it will be closer to the fraction of your balance. It should always be between these two numbers.

(Manifold also has loans which complicates things, the lower bound is actually on the Kelly fraction of (balance minus loans))

Sorry if it's confusing that in the post I'm using "the Kelly criterion" to mean maximising expected log wealth, whereas some other places use it to mean literally betting according the formula f = p - q/b. I prefer to use the broader definition because "the Kelly criterion" has a certain ring to it 😌, this is also the definition people on Lesswrong tend to use.

Simon_M2y2

Basically it simulates the possible outcomes of all the other bets you have open.

How can I do that without knowing my probabilities for all the other bets? (Or have I missed something on how it works?)

Will Howard🔹2y3

It assumes the market probability is correct for all your other bets, which is an important caveat. This will make it more risk averse than it should be (you can afford to risk more if you expect your net worth to be higher in the future).

It also assumes all the probabilities are uncorrelated, which is another important caveat. This one will make it less risk averse than it should be.

I'm planning on making a version that does take all your estimates into account and rebalances your whole portfolio based on all your probabilities at once (hence mani–folio). This is a lot more complicated though, I decided not to run before I could walk. Also I think the simplicity of the current version is a big benefit, if you are betting over a fairly short time horizon and you don't have any big correlated positions then the above two things will just be small corrections.

Daniel Hnyk2y2

Cool tool! Thanks for doing this.

Also, I want to appreciate the focus on the user (e.g. being very cautious about adding something that is gonna complicate the usage). You have successfully resisted the temptation 😁!

sam_brenner2y2

One idea: would it be possible to have a limit order mode? This would be useful I think!

Will Howard🔹2y3

I would really like to add some kind of limit order mode. I also often set up a limit order to sell out of my position once I have reached a certain profit which I would like to be able to do via the calculator.

The main reason I haven't done this, and the thing suggested by @Matthew_Barnett below of adding a discount rate, is that I wanted to keep this very simple so that people aren't overwhelmed by settings. I think the cost of adding an additional setting is quite high because:

A lot of people will be put off and literally just click away if there are too many settings, and then go back to making worse bets than if they only been shown a subset of those settings
People (me) will waste time fiddling with settings that aren't that important, and either end up making worse bets or just not benefit that much for the extra cost (or think "ugh I have to estimate the expected resolution time in both the YES and NO case" when they see a favourable market, and just not bet on it instead). The discount/expected growth rate is very susceptible to this I think, because it's easy to be overconfident and avoid ok bets because of the perceived opportunity cost (especially as your growth rate will go down as your balance goes up and it's harder to find markets that can absorb all your mana, so people are likely to overestimate their long term growth rate)
On the practical side, every extra setting increases the chance of bugs, and being pretty confident that the answer is correct is important for a calculator that makes important decisions for you

My current plan is to leave this calculator basically as is, and built another more fully featured one for advanced users, which will hopefully include these things:

Accounting for several estimates at the same time, and remembering previous bets
Time discounting (which overlaps with the one above)
Limit orders, or some other way of automatically buying in/out of a position over time
Estimating the resolution time in each outcome (this is important if you have a market like "Will Donald Trump tweet before the end of 2023", where it can resolve YES early but can't resolve NO early. It changes the ROI quite a bit)

I'm not 100% sure this is the right approach though, because I could throw some of these things in "Advanced settings" pretty easily (within a week or two), whereas building the better thing would take at least a couple of months. I'd be interested in your thoughts on this seeing as you're an actual real user!

sam_brenner2y2

I think I'm much more interested in the limit order mode than any of the other features you mentioned, so if there's room for a single additional setting inside the current calculator, I'd want it to be that one. However, I agree with your general thoughts on the cost of additional features, and all the other ones you mention do seem useful!

sam_brenner2y2

The way I imagine this working is that the tool could make its normal slippage assumptions until the limit is hit, and no more slippage after that

NunoSempere2y-1

Nice!

[comment deleted]2y1

Deleted by Dane Valerie, 08/11/2023

Reason: As requested by Saheb through intercom