This is a less formal overview of the key ideas in the working paper “Bracketing Cluelessness”. There is also a standalone linkpost for the paper, which I’ve split off from this post, since this one contains personal commentary (not necessarily endorsed by my co-authors).
Summary
- We may be clueless about how our actions affect aggregate welfare: we may not be able to say any intervention is better, worse, or exactly as good as another, in terms of its expected total consequences. There is an intuition that the appropriate response is to base our decisions on relatively robust and predictable effects, and that this favors near-term interventions like global health and animal welfare. But there is not yet a principled basis for this move that also respects impartial, risk-neutral consequentialism.
- In a new paper, colleagues and I try to fill this gap with a new theory of decision-making: bracketing. Bracketing says to base our decisions on those consequences we are – in a precise sense – not clueless about, “bracketing out” the others. The idea is that the effects we’re clueless about should not override the obligations given to us by the benefits we aren’t clueless about, like the immediate benefits of malaria nets to the global poor. Thus bracketing could provide action-guidance in the face of cluelessness and in particular support neartermism.
- To be clear, bracketing isn’t a heuristic to help boundedly rational agents maximize total expected utility. It is a distinct normative theory from expected total utility maximization.
- After an informal explanation, I give the formal definition of bracketing, and then discuss some of the major challenges it faces:
- There may be multiple ways of grouping “the consequences we’re not clueless about”, and these may give conflicting recommendations, in which case bracketing (at least the version we present) won’t be any more action-guiding than standard consequentialism.
- To formalize the “effects” of actions, so that we can talk about which ones we are and aren’t clueless about, bracketing requires us to specify the “locations of value”. These might be persons, spacetime regions, or something else. It turns out that neither persons nor spacetime regions is a great option (though unfortunately a proper discussion of why is out of scope for the post and paper).
- Bracketing will sometimes rank actions in a cycle, i.e., there are cases where according to bracketing, . While this is an unappealing property at first glance, I discuss three versions of this objection and why we don’t find them worrying. (This discussion is in an appendix since it’s more technical.)
- We don't have a satisfactory account of how bracketing should work when we face a sequence of decisions over time, as we do in real life. (In particular, we need to be able to reason about the value of information: when should I gather information that might change how bracketing evaluates future decisions?) In our discussion of cyclicity, we do give a sequential version of bracketing (and show how it avoids “value-pumps”), but that isn't the final word.
- I touch on other possible implications:
- Bracketing may provide a more satisfying story for why and when we should get off the train to crazy town (e.g., disregard acausal effects outside our lightcone).
- The formal apparatus of bracketing isn’t inherently tied to “locations of value”. I discuss directions for applying the idea of bracketing to normative uncertainty, where we are clueless about the implications of certain normative theories and it seems like we ought to bracket those views out.
Introduction
If most of the value we can influence is in the far future, why should impartial, risk-neutral altruists work on interventions like buying malaria nets or improving animal welfare? For example, here is Alexander Berger, CEO of Open Philanthropy, explaining his sympathies with the neartermist work which makes up much of Open Phil’s portfolio:
I’m very sympathetic to the idea that ethical value is [...] vastly loaded out into the far future. And then I think the follow-up claim that I’m a lot more skeptical or uncertain of is that it should guide our reasoning and actions. It just strikes me as totally plausible that our ability to reason about and concretely influence those things is quite limited.
This can’t be the whole story, because our ability to reason about the long-run effects of near-term interventions is quite limited, too. So it isn’t clear why we should think that neartermist work might be the best way to improve the world, or even net-positive, rather than acknowledging that we are clueless. (Berger himself apparently recognizes this.) We could ignore the potential effects that are “too speculative”, leaving only the near-term effects to base our assessments on.[1] While there is a strong pull to this view, there’s no rigorous proposal for how and why we ought to do this that still respects a commitment to impartial, risk-neutral consequentialism.
In a new working paper, colleagues and I try to fix that. We present a new theory[2] of how we ought to make altruistic decisions, which we call bracketing. Bracketing tells us to separate the effects of our actions into those we’re clueless about and those we aren’t, and to base our decisions on the latter. The driving intuition, for me, is that cluelessness about some effects (like those in the far future) doesn’t override the obligations given to us by the benefits we’re not clueless about, such as the immediate benefits of our donations to the global poor.
Bracketing could thus have serious implications for real-world altruists, in particular, vindicating the classic effective altruist focus on near-term interventions. We aren’t fully sold on bracketing, though. For my part, this is largely because it’s a new philosophical idea that probably has important problems we haven’t thought of yet. Plus, I’m pretty worried about the problem of how to choose the locations of value (more), and somewhat worried about getting a reasonable theory of sequential decision-making (more). But:
- I think it’s big-if-true. Indeed, even if it’s not so satisfying in absolute terms, it still may be among the best theories we have, if we take both consequentialism and cluelessness seriously.
- We don't otherwise have a good theory to justify ignoring some of the effects of our actions, despite the apparently common and influential intuition that we should do so. Even if I decide that bracketing is not a good enough justification either, it makes an important contribution: It helps us to understand what such a theory would need to look like, and what costs it would have.
- Bracketing may have important applications beyond consequentialism, such as providing greater action-guidance under normative uncertainty.
The basic idea
We start from a place of cluelessness about the effects of our actions on aggregate, cosmos-wide value. Our uncertainty is so deep that we can’t even say whether we expect one action to be better than, worse than, or just as good as another, in terms of its effects on aggregate utility. (See Section 2 of the paper and resources here for arguments as to why we ought to regard ourselves as such.) Does that mean there’s no reason to do anything on the basis of impartial consequentialism? Not so fast.
Take Mogensen's (2020) example of deciding whether to donate to the Against Malaria Foundation (AMF) or the Make-a-Wish Foundation (MAWF). As Mogensen argues, you’re clueless about the overall effects of donating to AMF vs. MAWF, due to their highly ambiguous effects on population dynamics, economic growth, resource usage, etc. You can come up with lots of asymmetrical effects each intervention has on total value, and you don’t have any principled way of weighing them up, but they still may swamp the immediate effects. Thus it seems that each of the available actions – Donate to AMF, Donate to MAWF, or Do Nothing – is permissible.
And yet, if you’re like me, you suspect that even an impartial consequentialist ought to choose AMF. For we aren’t clueless about the effects of our actions on the immediate beneficiaries! Restricting attention to those who would be prevented from contracting malaria by an AMF donation and the child who would be granted a wish by an MAWF donation, we can rank our actions by their expected total value: AMF MAWF Do Nothing. So my thought is, “Those immediately affected, who I’m not clueless about, give me a reason to Donate to AMF. It is true that, once I start accounting for more moral patients, I’ll become clueless about total value. But my cluelessness about this enlarged set of patients does not override the reasons given to me by the immediate beneficiaries. So, still, I’m required to Donate to AMF.” And that's the essence of bracketing.
To be clear, this isn’t a heuristic to help boundedly rational agents maximize total expected utility. It is a distinct normative theory from expected total utility maximization.
In the paper, we talk about “top-down” and “bottom-up” versions of bracketing, but we end up favoring “top-down”. So, I’ll just talk about that version in this post, and refer to it as “bracketing”.[3] Bracketing is defined like this:
Bracketing relation, informal. In a choice between actions and , you should base your decision on the effects on a set of beneficiaries such that (i) you’re not clueless about how to compare those beneficiaries’ total value under vs. , and (ii) there’s no way of adding more beneficiaries to this set without becoming clueless about the total value for the beneficiaries in the set. I.e., you make a decision by bracketing everything outside of .
In our example, we’re not clueless about the effects on the potential malaria victims and the sick child. We’re clueless about everyone else. So the bracketing relation sets aside everyone besides these immediately-affected patients, resulting in the ranking AMF MAWF Do Nothing.
This informal discussion raises a bunch of questions, like:
- Is the set of beneficiaries that aren’t bracketed out always unique? (In the AMF vs. MAWF case there’s a single maximal group we can focus on without becoming clueless. However, in more complex cases, could there be multiple such groups?)
- Who or what exactly are these “beneficiaries”, anyway? (In the AMF vs. MAWF case the “beneficiaries” are persons, but this assumption isn’t required and it might not be the best choice.)
- Does an agent making decisions based on bracketing generally behave in sensible-looking ways?
I’ll say more about these in the next section, where I’ll discuss some of the key ideas from the paper with a tad more formalism.
In more detail: Formalism and major challenges
Cluelessness and imprecise probabilities
We need to say specifically what we mean by “cluelessness”. We’ll model it using imprecise probabilities. In this framework, our beliefs are represented not by a single probability distribution, but a set of probability distributions, which we’ll call . The expected total value given an action is also imprecise; each precise probability distribution in gives us a different expected total value.
Since we're representing our beliefs with not just one probability distribution but a set of distributions, we can only say that action is at least as good as action if it is true for all of the probability distributions in set . If any of these distributions disagree (that is, the expected total value of action is higher than that of action for some but lower in others) then action is incomparable to action . This incomparability is what we mean when we say that we're clueless as to whether is better than .
Defining bracketing
Bracketing tells us to restrict our attention to those consequences we’re not clueless about, so we need to be clear about what “consequences” are. To formalize “consequences”, we introduce a set of locations of value. The locations of value might stand for a set of persons or spacetime locations, for example. (This idea of “locations of value” isn’t original to us. It crops up in infinite ethics, for example, which we touch on below.) The way we define our locations of value determines how we individuate the “expected consequences” of our actions:
- If a location of value is a person, then the expected utility at that location is the expected total value of that person’s life. In the AMF vs. MAWF example, such “locations” include the potential malaria victims and the sick child;
- If a location of value is instead a small spacetime region, the expected utility at that location is instead the expected total welfare of the experiences had in that region (in general experienced by different minds which exist at that location in some possible world). In the AMF vs. MAWF example, a relevant subset of locations are those regions of spacetime which would contain the malaria victims and the seriously ill child.
(Figuring out what the locations of value ought to be is a central hurdle for a satisfying theory of bracketing. More on that in a minute.)
The total utility of a world will then be the sum of the value at each of the locations of value in that world. Similarly, we can define the total utility over subsets of locations of value. This is what allows us to talk about not being clueless about some of the effects of our actions.
We can then formalize the definition of bracketing given in the previous section. Let’s use the comparison of donating to AMF and MAWF as an example. Take the set of all beneficiaries to be I ={potential malaria victim 1, potential malaria victim 2, sick child, indirectly affected person 1, indirectly affected person 2, ...}. We first want to look for the subsets of beneficiaries about which we aren’t clueless, which we refer to as bracket-sets. Formally:
Bracket-set. A bracket-set relative to actions is a set such that we’re not clueless about whether or has a greater expected total utility for the locations in .
Relative to Donate to AMF and Donate to MAWF, {sick child} is a bracket-set, since I expect MAWF to be better for the sick child than AMF. (In fact, every subset of {potential malaria victim 1, potential malaria victim 2, sick child} is a bracket-set.)
The fact that is better than on some subset of locations of value is a reason to favor , and this cannot be overridden by cluelessness about further consequences. But it can be overridden if we aren't clueless about the relative goodness of and when accounting for more consequences. This leads us to look at maximal bracket-sets::
Maximal bracket-set. is a maximal bracket-set if is a bracket-set and there is no bracket-set strictly containing .
So maximal bracket-sets are those whose ranking of and can't be overridden, in the above sense, by considering more consequences. Adding more consequences can only render us clueless about the comparison of and .
Continuing with our example: Let’s assume that, for any “indirectly affected person N”, we’re clueless about whether Donate to AMF or Donate to MAWF yields higher total utility for the immediate beneficiaries plus that person, i.e., {potential malaria victim 1, potential malaria victim 2, sick child, indirectly affected person N}. (This isn’t a realistic assumption, but it doesn’t matter for the purposes of illustration.) This means that {potential malaria victim 1, potential malaria victim 2, sick child} is a maximal bracket-set. First, it’s a bracket-set: Looking only at these beneficiaries, I am not clueless about total expected value, as I expect AMF to lead to more total value than MAWF. Second, there’s no way to account for more beneficiaries without becoming clueless.
This is all depicted in Figure 1. The green dots are potential malaria victims, the red dot is the sick child, the grey dots are everyone else, and the red and green dotted ovals are non-maximal and maximal bracket-sets, respectively.
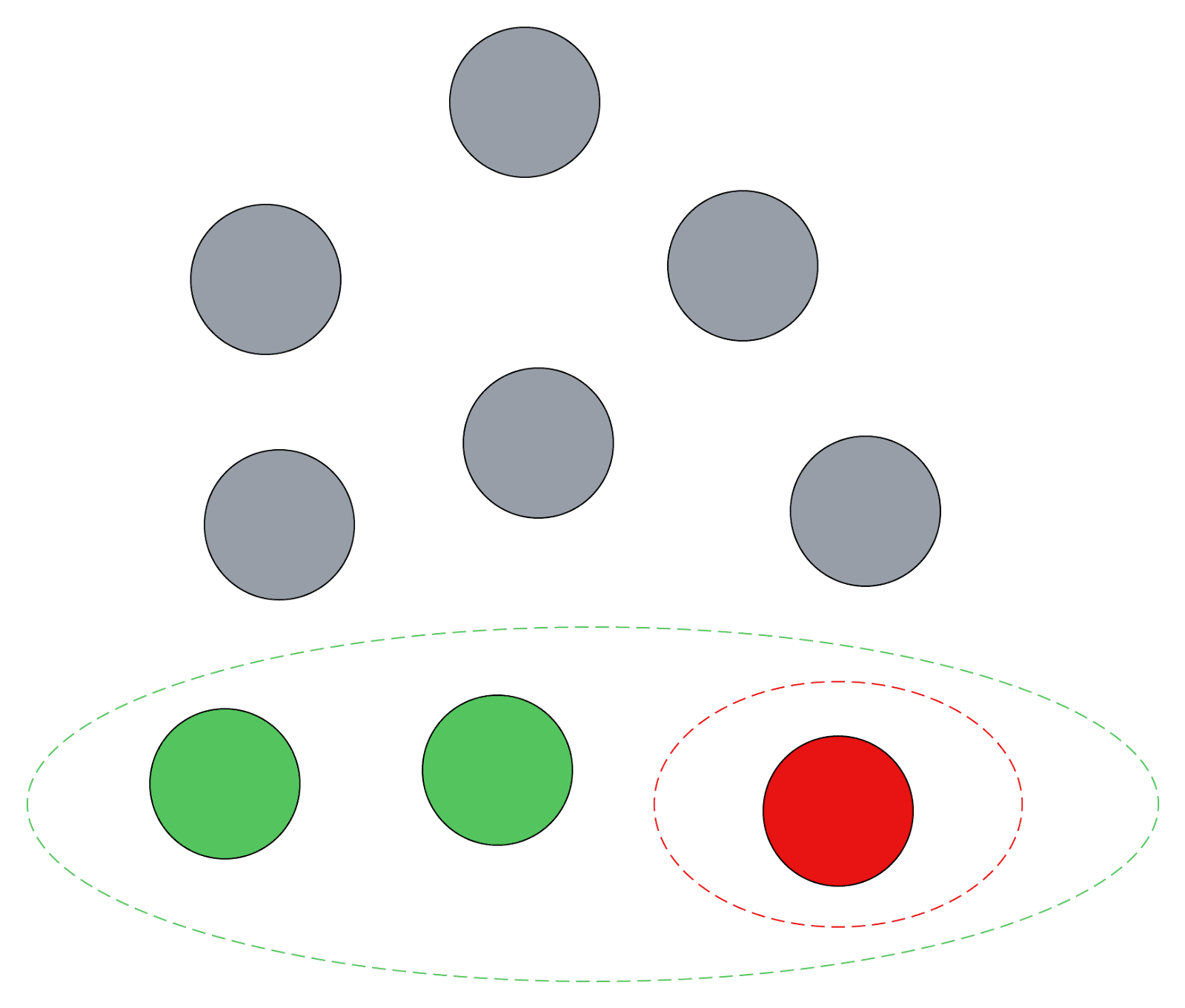
In this case, there is only one maximal bracket-set. But it's possible for there to be multiple maximal bracket-sets. How do we choose in such cases? Maybe there are better ways of doing it, but a natural solution in such cases is to rank over whenever is better than for all maximal bracket-sets. Thus our definition of the (top-down) bracketing relation is[4]
Bracketing relation. Bracketing ranks above if has higher expected utility than for all maximal bracket-sets.
It could turn out that there are conflicting maximal bracket-sets for each pair of actions we're considering. In that case, bracketing would provide no more action-guidance than standard consequentialism. An example inspired by recent Effective Altruism Forum discourse (e.g., here): Consider an intervention to reduce the consumption of animal products. This prevents the terrible suffering of a group of farmed animals, call them . But, perversely, it may increase expected suffering among wild animals, call them . This is because farmed animals reduce wild animal habitat, and wild animals may live net-negative lives, so that preventing their existence might be good. But we are clueless about the total effects accounting for and together (and we are clueless about the total other effects, too). So, we can construct a maximal bracket-set favoring the dietary change intervention by taking the locations of value in , or we can construct a maximal bracket-set favoring not doing the dietary change intervention by taking those in .[5]
(I don’t claim that this is the correct analysis of any real-world intervention, it’s just an example.)
However, if there don’t end up being conflicting maximal bracket-sets, it should be clear how bracketing would tend to support neartermism. This doesn’t mean that we can stop worrying about flow-through effects, though, a point I’ll briefly return to in the conclusion.
For now, we’ll turn to some of the theoretical challenges for bracketing.
Theoretical challenges
What are the locations of value?
A complete theory of bracketing should tell us what the locations of value are, and why. There are various ways these could be chosen, and they may result in different recommendations. I’ll talk about two leading contenders: persons and spacetime locations.[6]
It looks to me like bracketing with spacetime locations has a much better shot at being action-guiding than bracketing with persons. Despite the importance of this point, a proper discussion is beyond the scope of this post and our paper, though I've tried to put some intuition in a footnote.[7]
If it’s true that only spacetime location-based bracketing is action-guiding, that’s unfortunate, because spacetime locations don’t seem morally relevant! (You might or might not consider persons to be morally relevant – maybe they, too, are just containers of experience-moments – but spacetime locations definitely don’t seem to be.) We would be left with a tradeoff: Morally well-motivated but doesn’t get the intuitive answers in terms of action-guidance (persons) vs. morally poorly-motivated but gets the intuitive answers (spacetime locations). I don’t know what the right answer is, but I am open to the idea that spacetime bracketing is the best we can do.
Interestingly, this is closely analogous to the situation in infinite ethics. Prominent theories of infinite ethics also depend on locations of value. (For example, we might want our theory to satisfy a “Pareto principle” which says that an infinite world World 1 is better than another World 2 if it is better than World 2 at each location of value.) And it turns out that theories of infinite ethics based on persons also lead to much more widespread incomparability than those based on spacetime locations (Askell (2018), Wilkinson (2021)).[8] The implausibility of incomparability in the cases he considers leads Wilkinson to develop an approach to infinite ethics based on spacetime locations. We may have in infinite ethics a surprising source of support for spacetime bracketing?
Cyclicity
The main objection we address in the paper is that the bracketing relation may have cycles. That is, if is the bracketing relation, there are cases where actions are ranked as .
It’s a common feeling that this is a nasty property for a ranking to have. We discuss three different versions of the cyclicity objection, however, and conclude that none of them is so problematic. (And note that we are not the first to argue that cyclicity is not a fatal objection to using some ranking as a basis for choice. See, e.g., Thoma (2024) and references in Section 6.1 of our paper.) This discussion requires us to get more technical, so I defer a synopsis of the objections and our responses to the appendix.
Sequential decision-making
I’ve talked about bracketing in one-off decision problems. But we need to make decisions over time, accounting for how our beliefs may change in the face of new evidence. For example, how do I decide whether to do prioritization research that could update my beliefs in a way that changes my maximal bracket-sets, versus choosing an intervention based on my current beliefs?
We don't have much of an answer to this yet. To respond to one version of the cyclicity objection, the “value-pump” objection, we do give a generalization of bracketing to the sequential decision-making setting. I think it’s a good starting point, but it wasn’t designed to handle the possibility of information that would change our maximal bracket-sets, so it needs more work.
Further implications of bracketing
I’ve focused on what bracketing says about neartermism. But bracketing may have other important ramifications; I'll touch on a few here. For the most part, we don’t get into these points in the paper.
Getting off the train to crazy town: Why and where
At the start, I suggested that the practice of disregarding long-term effects and focusing on the near-term has (at least for impartial, risk-neutral consequentialists) not been well-motivated. But neartermists aren’t the only ones who could be accused of restricting the scope of their assessments in an ad hoc way.
Longtermists tend to focus on all the value in the stars that humanity can directly access by colonizing space (“the lightcone”). Yet there might be vastly more value still from exotic possibilities like acausal influence on causally disconnected parts of the cosmos! Even if one thinks these are unlikely, the huge amount of utility at stake if they end up making sense could mean that they swamp a consequentialist expected value calculation.[9] Yet, my sense from personal experience is that many who are bought into longtermism on the grounds of risk-neutral, impartial consequentialism effectively ignore these possibilities because of their absurdity. See also this discussion of the effective altruist inclination to “get off the train to crazy town”.
As with ignoring long-term effects, bracketing may be able to back up the intuition that we shouldn’t be basing our decisions on exotic possibilities for impact. We might reasonably think that we are clueless about the effects of our actions on distant parts of the cosmos, in which case bracketing would (assuming we can identify “distant parts of the cosmos” with a distinct set of locations of value) tell us to bracket them out.[10] We would not be ignoring these possibilities just because they are “speculative”, but because we have no idea how to assess their consequences, and we have a clear account for how to bracket such consequences out of our decision-making.
Needless to say, longtermists who bracket out, e.g., acausal effects should have a story for why they should not get off the train to crazy town earlier, bracketing out the non-exotic long-term effects, too.
Bracketing beyond locations of value
The machinery of bracketing is not specific to locations of value, or to consequentialist aggregation in general, and we might wonder how else it could be applied. I’m especially excited about bracketing as applied to normative uncertainty and pluralism, which my colleague Anthony DiGiovanni has developed, and hopefully will write more about soon. Suppose we have several normative theories we want to put some weight on, and we choose actions by somehow aggregating the recommendations of these theories. For concreteness, let's take the “expected choiceworthiness” (MacAskill and Ord 2020) approach. Expected choiceworthiness assumes that each normative theory gives a "choiceworthiness" score to each action, and expected choiceworthiness is the average of such scores taken with respect to our credences in each of the theories.
What happens if we allow theories to have imprecise choiceworthiness scores, as would be the case with the imprecise probability version of consequentialism we've discussed here? These could “infect” the expected choiceworthiness calculation, leaving all the available actions with indeterminate expected choiceworthiness. Say my two normative theories are “consequentialism with imprecise beliefs” and “commonsense morality”. The cluelessness from consequentialism with imprecise beliefs could make the weighted average of these two theories’ judgements of choiceworthiness indeterminate, leaving us totally morally clueless. We would be clueless even about actions that are obviously evil (and thus in violation of commonsense morality). (Also see MacAskill (2013) on the “infectiousness of nihilism”.)
But bracketing may come to the rescue! We may want to bracket out the normative views that are infecting our expected choiceworthiness, basing decisions on maximal bracket-sets of normative theories. In the example above, that means bracketing out imprecise consequentialism and making decisions based on commonsense morality.
Conclusion
My co-authors and I have presented bracketing, a new theory of altruistic decision-making in the face of cluelessness. Bracketing might provide a foundation for common neartermist intuitions and more generally the reasonableness of setting aside “speculative” considerations, where a foundation has been lacking. On the other hand, bracketing faces considerable challenges and, as a novel philosophical proposal, requires further scrutiny.
Finally: If we did ultimately endorse bracketing, it wouldn't mean that we could always base our decisions on the proximal or immediately obvious consequences of our actions; it wouldn’t absolve us from thinking about knock-on effects, which unfortunately afflict the analysis of near-term interventions even under bracketing. What if saving the lives of the global poor leads to more meat-eating and thus more farmed animal suffering? What about the effects on wild animals? The answers to these questions affect the composition and recommendations of our maximal bracket-sets and so can’t be ignored.
Acknowledgements
Commenters on drafts gave many helpful suggestions which made the post much more readable. Thanks very much to Joseph Ancion, Daniel Barham, Jim Buhler, Alex Cloud, Luke Dawes, Anthony DiGiovanni, Vasco Grilo, Sylvester Kollin, and Magnus Vinding.
References
Askell, Amanda. 2018. “Pareto Principles in Infinite Ethics.” https://philpapers.org/rec/ASKPPI.
Greaves, Hilary. 2016. “XIV—Cluelessness.” Proceedings of the Aristotelian Society 116 (3): 311–39.
MacAskill, William. 2013. “The Infectiousness of Nihilism.” Ethics 123 (3): 508–20.
MacAskill, William, and Toby Ord. 2020. “Why Maximize Expected choice‐worthiness?1: Why Maximize Expected Choice-Worthiness?” Nous (Detroit, Mich.) 54 (2): 327–53.
Meacham, Christopher J. G. 2012. “Person-Affecting Views and Saturating Counterpart Relations.” Philosophical Studies 158 (2): 257–87.
Miller, Nicholas R. 1980. “A New Solution Set for Tournaments and Majority Voting: Further Graph- Theoretical Approaches to the Theory of Voting.” American Journal of Political Science 24 (1): 68.
Mogensen, Andreas L. 2020. “Maximal Cluelessness.” The Philosophical Quarterly 71 (1): 141–62.
Rabinowicz, Wlodek. 1995. “To Have One’s Cake and Eat It, Too: Sequential Choice and Expected-Utility Violations.” The Journal of Philosophy 92:586–620.
Thoma, Johanna. 2024. “Preferences: What We Can and Can’t Do with Them.” Philosophia (Ramat-Gan, Israel), November. https://doi.org/10.1007/s11406-024-00794-6.
Wilkinson, Hayden. 2021. “Infinite Aggregation.” Australian National University. https://scholar.archive.org/work/3fcsebsepbb2rnqa2s6caa2m5i/access/wayback/https://o penresearch- repository.anu.edu.au/bitstream/1885/238242/1/Wilkinson%20Thesis%202021.pdf.
Appendix: More on cyclicity
Example of a cycle
In Section 6.1 of the paper we give an example of a case where the bracketing relation exhibits a cycle. This case is summarized in Table 1 below in a way that makes it easier to see why there is a cycle. Table 1 shows the (imprecise, and therefore interval-valued) differences in expected total utilities for each pair of actions, at each subset of locations of value.
Table 1. The cycle in Section 6.1 of the paper. There are two locations of value, 1 and 2, and three actions, . The values in the cells represent the difference in precise expected values for a particular pair of actions, at a subset of locations. Write as the expected utility at location under precise probability distribution , given action . Then, for example, the interval in the cell on row “ minus ” and column {1, 2} is given by which is equal to . In this case, the interval representing the imprecise difference in expected utilities contains numbers on each side of zero, so it’s indeterminate whether A or is better at locations of value {1, 2}.
| {1} | {2} | {1,2} | |
| A minus B | [1,1] | [-18,8] | [-17,9] |
| B minus C | [1,1] | [-18,10] | [-17,11] |
| C minus A | [-2,-2] | [8,10] | [6,8] |
Here’s how bracketing applies to this case:
- {1} is a maximal bracketing relative to and , and favors .
- {1} is a maximal bracketing relative to and , and favors .
- {1,2} is a maximal bracketing relative to and , and favors .
Thus we have a cycle in which . This arises from the fact that different locations of value are bracketed out when comparing different pairs of actions.
Versions of the objection from cyclicity and our responses
The semantic argument
Maybe part of what it means for a relation to capture “betterness” is for it to be acyclic. In that case, the bracketing relation can’t be a betterness relation.
Our reply: We don’t take a stance on the semantics of “better than”. (Some have famously argued that “better than” is intransitive after all.) Regardless, we can interpret the bracketing relation in terms of choiceworthiness rather than betterness. It is possible that I ought to choose over even if isn’t better than .
In the AMF vs. MAWF example, is preventing several children from getting malaria “better” than fulfilling one sick child’s wish on account of the immediate beneficiaries? I don’t know. But it could be that we still ought to choose AMF over MAWF in a head-to-head comparison, because of what we said before: The immediate beneficiaries give me a reason to choose AMF over MAWF, and this is not overridden by other reasons.
The synchronic (one-off) choice argument
If , , and form a cycle, how are we even able to make choices in a one-off decision? We can’t say “choose an action that isn’t ranked lower than some other action”, because they’re all ranked lower than some other action!
Our reply: Seems like you just need the right choice rule. We give an example of an attractive choice rule – the “Uncovered Choice Rule” (Miller 1980) – that allows agents with cyclic preferences to make choices fine. Relative to a ranking , covers if (i) and (ii) whenever , it’s also the case that . The Uncovered Choice Rule says that any uncovered action is permissible to choose. It turns out that the set of permissible outcomes under this rule is never empty.
(This reply to the synchronic choice argument isn’t original to us. See, e.g., Thoma (2024, 1272).)
The dynamic choice (value-pump) argument
And finally there is the charge that agents with cyclic preferences are liable to be value- (“money-”)pumped.
To respond to this, we need to say how bracketing is supposed to work in settings with sequences of choices (“dynamic choice”) like would-be value-pumps. In the paper, we give a generalization of bracketing to dynamic settings which avoids value-pumps.
This one’s especially in-the-weeds, but here’s the thrust of it. The question is, which policy to follow in a sequential decision problem? Plausibly, consequentialism – i.e., doing well according to (imprecise) expected total utility – should take precedence over bracketing. So we first restrict to the set of policies that can, in some sense, realistically be performed – i.e., are “feasible” – under imprecise consequentialism. And we think that any plausible extension of imprecise consequentialism to the sequential setting will rule out value-pumps. (In particular, a plausible theory of dynamic consequentialist choice is something called “wise choice” (Rabinowicz 1995). “Wise” policies don’t get value-pumped when based on an incomplete but transitive relation, which imprecise consequentialism is.)
We then choose our policy by applying bracketing to this restricted set of policies. Instead of comparing individual actions based on the bracketing relation, we compare entire feasible policies. We then apply an appropriate choice rule – like the Uncovered Choice Rule – to get our policy. Because none of the feasible policies get value-pumped, our policy doesn’t get value-pumped.
We’re not confident that this is the best way to generalize bracketing to the dynamic setting. One thing is, the rule picks a maximal bracket-set to base decisions on at the beginning of the decision problem, and never revises it. But that might be wrong, and the bracket-set on which decisions are based should sometimes change based on changes in beliefs. Still, even if some other generalization is better, as long as it can be combined with wise choice it won’t be value-pumpable.
- ^
One could try to argue that the second-order effects of near-term interventions are negligible in expectation (see "the washing out hypothesis"). But I don’t think this is plausible. For one thing, even very small effects on the probabilities of "lock-in" events would result in huge contributions to total expected utility, given the enormous numbers of future beings affected by lock-in events.
- ^
There are various other proposals which restrict the scope of consequentialism or discount some effects in a way that could ameliorate cluelessness, but none seem satisfactory. One could discount effects as a function of their distance in space and time, but this is at odds with impartiality. One could ignore effects with sufficiently small probabilities, but this requires us to make an arbitrary choice as to what probability is “too small”. And, in any case, neither of these proposals capture the intuition that bracketing is trying to capture. These articles discuss versions of consequentialism based on “reasonably expected” or “reasonably foreseeable” consequences, which might be more like what bracketing is trying to do, but as far as I know these haven’t been developed into a precise theory. (Thanks to Magnus Vinding for pointing these out to me.)
- ^
In contrast to top-down bracketing, bottom-up bracketing first sets aside those beneficiaries about whom we’re clueless. We end up rejecting it because it violates a “statewise dominance” criterion: I.e., it can be the case that in every state, has greater expected total utility than , and yet bottom-up bracketing doesn’t rank over .
- ^
Referred to in the paper as .
- ^
and aren’t maximal bracket-sets by themselves, because we can add locations of value to (say) to create a new set which still favors the dietary change intervention. What I mean specifically by “construct a maximal bracketing by taking the patients in ” is this: Start with ; add a location of value to to get a set which still favors the dietary change intervention; repeat until adding any more locations would leave you clueless, then stop. (Similarly, we can construct a maximal bracketing that speaks against the intervention starting with .)
- ^
Another direction is to specify a “counterpart relation” relating appropriately similar persons or experiences across worlds, even if they aren’t identical. This kind of move has been suggested in the context of the non-identity problem for person-affecting ethics (e.g., Meacham (2012)).
- ^
Personal identity is fragile, such that many persons exist only in worlds where we take a particular action. For example, personal identity depends sensitively on the timing of conception, and through many chaotic pathways our actions affect the times at which future persons are conceived. (The point may be familiar from the nonidentity problem for person-affecting ethics.) This creates a problem: we can construct a maximal bracket-set based on "all the happy people who would exist if we do " and another based on "all the happy people who would exist if we do ," where these sets favor different actions. Since bracketing only favors over if is better than for all maximal bracket-sets, this would leave us still indecisive between and .
Contrasting this with spacetime bracketing, take a given spacetime region . We could imagine it is part of Earth in the far future. has some chance of containing a happy person if we choose , and has some chance of containing a different (due to the fragility of personal identity) happy person if we choose . We are clueless about which person has a higher chance of existing, conditional on us taking their respective action. Thus we're clueless about whether or is better at . This leads us to bracket out, even though we could use the -person and -person inside to construct conflicting maximal person-based bracket-sets.
- ^
See Wilkinson’s Firing Line and saving-a-child-from-traffic cases.
- ^
- ^
Speculatively, bracketing might be important not only for our own decision-making, but for civilization in the long run. Possibilities like acausal trade could leave civilization indefinitely clueless about what to do, due to irreducible arbitrariness in weighing up the potential implications of such hypotheses. If that ends up being true, then a civilization might want to bracket out potential effects beyond our lightcone when deciding how to allocate its resources.

Thanks for writing this up and sharing. I find myself pretty sympathetic to the idea that people generally do better when they focus on the first order consequences of their actions and I appreciate this as a formalization of that intuition.
I interpret "support neartermism" to mean something like "donating to AMF is better than donating to AI safety." Is that what you mean? If so, do you have an example where this is true?
I buy that it's an argument against very crazy town actions like acausal trade, but most "longtermist" worldviews place a relatively high probability on e.g. AI killing a bunch of bed net recipients soon, so I would expect that you can't actually bracket out just the far future ones and find that AMF is c-better. (See e.g. EA and Longtermism: not a crux for saving the world.)
Thanks Ben — a few clarifications:
On your second point: Even if AI would plausibly kill the bed net recipients soon, we also need to say whether (1) any concrete intervention we’re aware of would decrease AI risk in expectation, and (2) that intervention would be more cost-effective for bracketed-in welfare than the alternatives, if so.
This will be obvious to Jesse, but for others:
Another important sense in which bracketing isn't the same thing as ignoring cluelessness is, we still need to account for unawareness. Before thinking about unawareness, we might have credences about some locations of value I' that tell us A >_{I'} B. But if the mechanisms governing our impact on I' are complex/unfamiliar enough, arguably our unawareness about I' is sufficiently severe that we should consider A and B incomparable on I'.
To be clear, you don't necessarily assume this in the paper, and you don't need to, right? You need bracketing to escape cluelessness paralysis, even if you merely think it's indeterminate whether most of the value we can influence is in the far future, afaiu.
So even if this were plausible (as Vasco thinks, for instance), this wouldn't be enough to think we don't need bracketing. One would need to have determinate-ish beliefs that rule out the possibility of far future effects dominating.
Bracketing is the most interesting recent idea in altruistic decision-making.
However, from the point of view of a sequential decision problem, an EV-maxing learner is more willing to make guesses about long-term, high-stakes effects and to learn from them, whereas a bracketing agent restricts itself to actions it is non-clueless about and may never learn about domains it brackets out–including the value of information itself. In this sense, bracketing seems to build a form of risk-aversion: it avoids speculative bets and forgoes opportunities to learn and adapt.
In practice, the main downside I see is that bracketers risk moving away from gaining influence over high-stakes uncertain problems and instead prioritize low-stakes neartermist interventions because of cluelessness about higher-stakes ones. As a result, bracketers may be overly conservative and lose influence relative to EV-maxers, who are more willing to make provisional guesses, risk being wrong, and update along the way.
(Edited to elaborate.)
I think bracketing agents could be moved to bracket out and ignore value of information sometimes and more often than EV-maxers, but it's worth breaking things down further to see when. Imagine we're considering an intervention with:
Then:
a. If the group in 2 is disjoint from the group in 1, then we can bracket out those affected in 1 and decide just on the basis of the expected value of information in 2 (and opportunity costs).
b. If the group in 2 is a subset of the group in 1, then the minimum expected value of information needs to be high enough to overcome the potential expected worst case downsides from the direct effects on the group in 1, for the intervention to beat doing nothing. The VOI can get bracketed away and ignored along with the direct effects in 1.
And there are intermediate cases, with probably intermediate recommendations.
As someone who's interested in the practical implications of cluelessness for practical decisions but would not be able to read that paper, I'm grateful that you went beyond a linkpost and took the time to make your theory accessible to more Forum readers. I'm excited to see what comes next in terms of practical action guidance beyond the reliance on EV estimates. Thank you so much for a great read!
How does the paper relate to your Reasons-based choice and cluelessness post? Is the latter just a less precise and informal version of the former, or is there some deeper difference I'm missing?
In principle the proposal in that post is supposed to encompass a larger set of bracketing-ish things than the proposal in this post, e.g., bracketing out reasons that are qualitatively weaker in some sense. But the latter kind of thing isn't properly worked out.
I feel this post is just saying you can solve the problem of cluelessness by ignoring that it exists, even though you know it still does. It just doesn't seem like a satisfactory response to me.
Wouldn't the better response be to find things we aren't clueless about—perhaps because we think the indirect effects are smaller in expected magnitude than the direct effects. I think this is probably the case with elevating the moral status of digital minds (for example).
It sounds like you reject this kind of thinking:
I don't think that's unreasonable. Personally, I strongly have the intuition expressed in that quote, though definitely not certain that I will endorse it on reflection.
The background assumption in this post is that there are no such interventions.
> We start from a place of cluelessness about the effects of our actions on aggregate, cosmos-wide value. Our uncertainty is so deep that we can’t even say whether we expect one action to be better than, worse than, or just as good as another, in terms of its effects on aggregate utility. (See Section 2 of the paper and resources here for arguments as to why we ought to regard ourselves as such.)
I do reject this thinking because it seems to imply either:
There's certainly a lot of stuff out there I still need to read (thanks for sharing the resources), but I tend to agree with Hilary Greaves that the way to avoid cluelessness is to target interventions whose intended long-run impact dominates plausible unintended effects.
For example, I don't think I am clueless about the value of spreading concern for digital sentience (in a thoughtful way). The intended effect is to materially reduce the probability of vast future suffering in scenarios that I assign non-trivial probability. Plausible negative effects, for example people feeling preached to about something they see as stupid leading to an even worse outcome, seem like they can be mitigated / just don't compete overall with the possibility that we would be alerting society to a potentially devastating moral catastrophe. I'm not saying I'm certain it would go well (there is always ex-ante uncertainty), but I don't feel clueless about whether it's worth doing or not.
And if we are helplessly clueless about everything, then I honestly think the altruistic exercise is doomed and we should just go and enjoy ourselves.
I'd recommend specifically checking out here and here, for why we should expect unintended effects (of ambiguous sign) to dominate any intervention's impact on total cosmos-wide welfare by default. The whole cosmos is very, very weird. (Heck, ASI takeoff on Earth alone seems liable to be very weird.) I think given the arguments I've linked, anyone proposing that a particular intervention is an exception to this default should spell out much more clearly why they think that's the case.
I'll read those. Can I ask regarding this:
What makes you think that? Are you embracing a non-consequentialist or non-impartial view to come to that conclusion? Or do you think it's justified under impartial consequentialism?
I have mixed feelings about this. So, there are basically two reasons why bracketing isn't orthodox impartial consequentialism:
I do think both of these are reasons to give less weight to bracketing in my decision-making than I give to standard non-consequentialist views.[1]
However:
E.g. compare (i) "A reduces x more units of disutility than B within the maximal bracket-set I', but I'm clueless about A vs. B when looking outside the maximal bracket-set", with (ii) "A reduces x more units of disutility than B within I', and A and B are equally good in expectation when looking outside the maximal bracket-set." I find (i) to be a somewhat compelling reason to do A, but it doesn't feel like as overwhelming a moral duty as the kind of reason given by (ii).
Thanks for the post, Jesse!
I think it is very important to keep this in mind. I think electrically stunning shrimp is one of the interventions outside research which more clearly increases welfare in expectation, and I would say it is still unclear whether it increases or decreases welfare in expectation due to effects on soil animals[1], and even more so accounting for microorganisms. However, very very little effort has been dedicated to understanding these. So I believe it makes all sense to remain open to the possibility of accounting for them.
The post you linked analyses the effects of chicken welfare reforms on wild animals. I have another one which looks into the effects of changing the consumption of animal-based foods.
For my individual welfare per animal-year proportional to "number of neurons"^0.5, I determined electrically stunning shrimp increases the welfare of these by 0.00144 QALY/shrimp. There are 94.3 shrimps per shrimp-kg. So infer electrically stunning shrimp increases the welfare of these by 0.136 QALY/shrimp-kg (= 0.00144*94.3). For my individual welfare per animal-year proportional to "number of neurons"^0.5, I estimate replacing farmed shrimp with farmed fish changes the welfare of soil ants, termites, springtails, mites, and nematodes by 364 QALY/shrimp-kg (= 522 - 158). So I conclude electrically stunning farmed shrimp changes the welfare of soil animals more than it increases the welfare of shrimps if it results in the replacement of more than 0.0374 % (= 0.136/364) of the consumption of the affected farmed shrimp by farmed fish. I can easily see this happening for even a slight increase in the cost of shrimp.