Knowing the shape of future (longterm) value appears to be important to decide which interventions would more effectively increase it. For example, if future value is roughly binary, the increase in its value is directly proportional to the decrease in the likelihood/severity of the worst outcomes, in which case existential risk reduction seems particularly useful[1]. On the other hand, if value is roughly uniform, focussing on multiple types of trajectory changes would arguably make more sense[2].
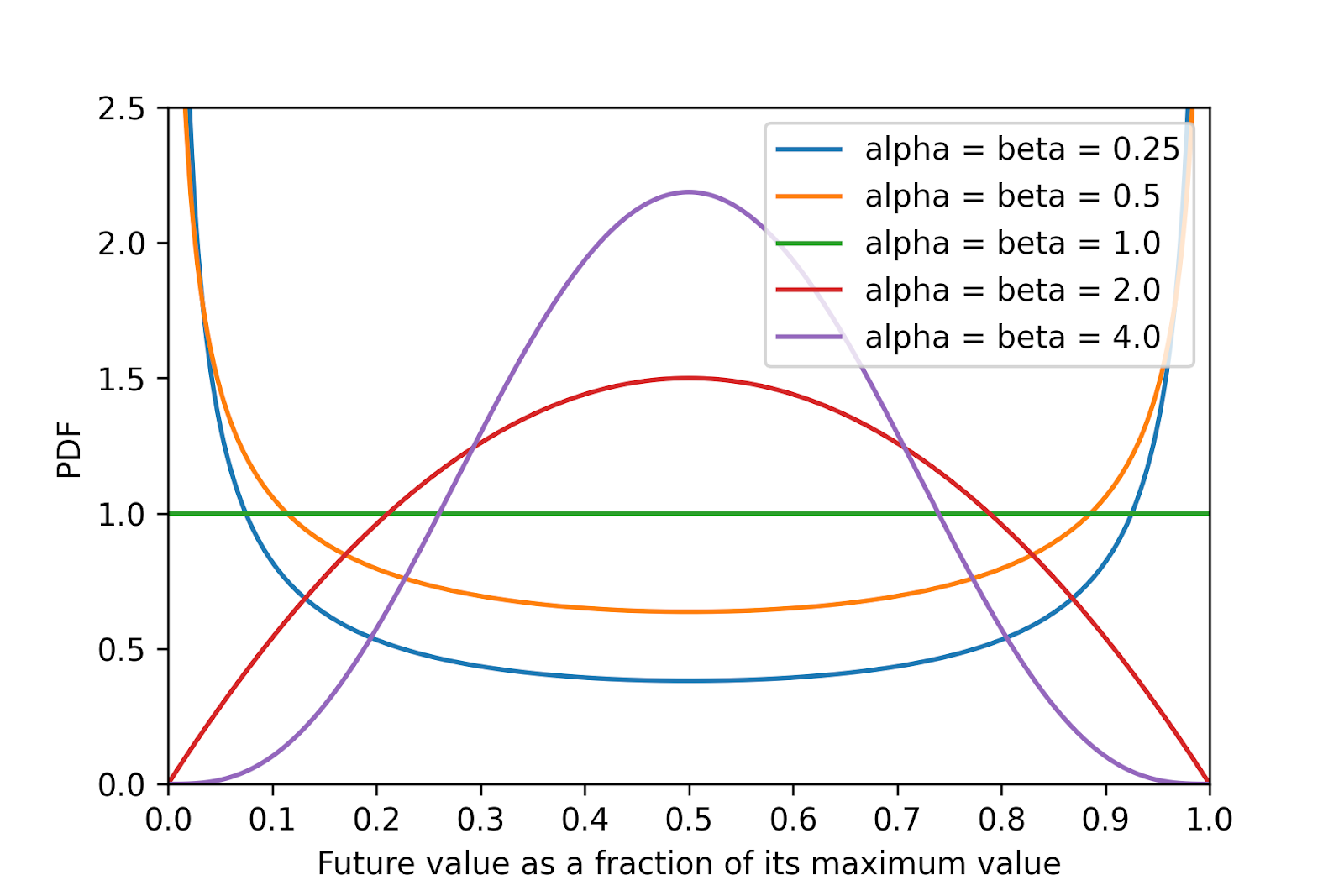
So I wonder what is the shape of future value. To illustrate the question, I have plotted in the figure below the probability density function (PDF) of various beta distributions representing the future value as a fraction of its maximum value[3].
For simplicity, I have assumed future value cannot be negative. The mean is 0.5 for all distributions, which is Toby Ord’s guess for the total existential risk given in The Precipice[4], and implies the distribution parameters alpha and beta have the same value[5]. As this tends to 0, the future value becomes more binary.
- ^
Existential risk was originally defined in Bostrom 2002 as:
One where an adverse outcome would either annihilate Earth-originating intelligent life or permanently and drastically curtail its potential.
- ^
Although trajectory changes encompass existential risk reduction.
- ^
The calculations are in this Colab.
- ^
If forced to guess, I’d say there is something like a one in two chance that humanity avoids every existential catastrophe and eventually fulfills its potential: achieving something close to the best future open to us.
- ^
According to Wikipedia, the expected value of a beta distribution is “alpha”/(“alpha” + “beta”), which equals 0.5 for “alpha” = “beta”.

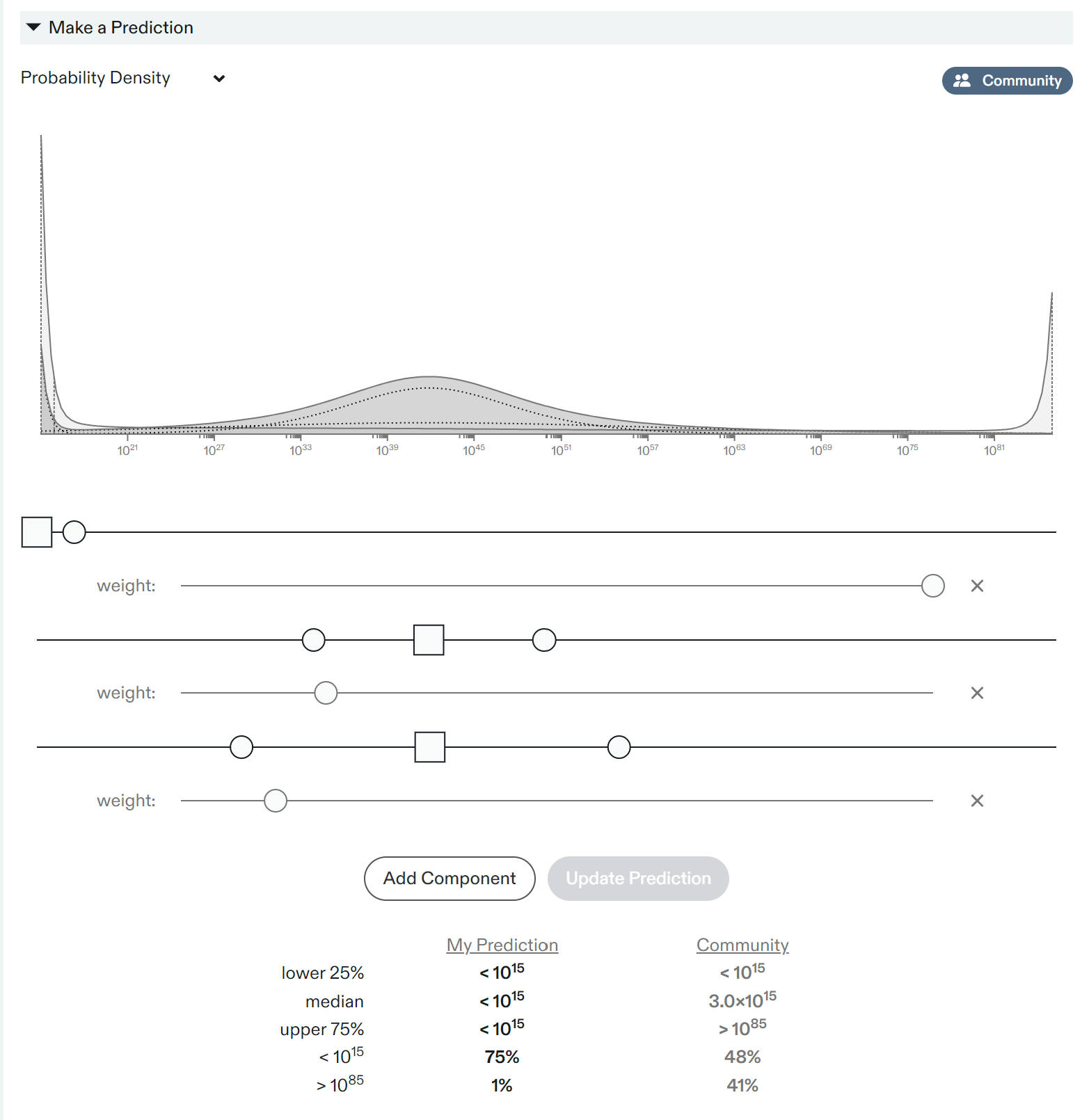
I think longterm value is quite binary in expectation.
I think a useful starting point is to ask: how many orders of magnitude does value span?
If we use the life of one happy individual today as one unit of goodness, then I think I think maximum value (originating from Earth in the next billion years, which is probably several orders of magnitude low) is around at least 10^50 units of goodness per century.
My forecast on this Metaculus question reflects this: Highest GWP in the next Billion Years:
My current forecast:
How I got 10^50 units of goodness (i.e. happy current people) per century from my forecast
I converted 10^42 trillion USD to 10^50 happy people by saying today's economy is composed of about 10^10 happy people, and such a future economy would be about 10^40 times larger than today's economy. If happy people today live 100 years, that gives 10^50 units of goodness per century as the optimal future a century from now.
I also of course assumed the relationship between GWP and value of people stays constant, which of course is highly dubious, but that's also how I came up with my dubious forecast for future GWP.
Is Value roughly Binary?
Yes, I think. My forecast of maximum GWP in the next billion years (and thus my forecast of maximum value from Earth-originating life in the next billion years) appears to be roughly binary. I have a lot of weight around what I think the maximum value is (~10^42 trillion 2020 USD), and then a lot of weight on <10^15 trillion 2020 USD (i.e. near zero), but much less weigh on the orders of magnitude in between. If you plot this on a linear scale, I think the value looks even more binary. If my x-axis was not actual value, but fraction of whatever the true maximum possible value is, it would look even more binary (since the vast majority of my uncertainty near the top end would go away).
Note that this answer doesn't explain why my maximum GWP forecast has the shape it does, so doesn't actually make the case for the answer much, just reports that it's what I believe. Rather than explain why my GWO forecast has the shape it does, I'd invite anyone who doesn't think value is binary to show their corresponding forecast for maximum GWP (that implies value is not binary) and explain why it looks like that. Given that potential value spans so many order of magnitude, I think it's quite hard to make a plausible seeming forecast in which value is not approximately binary.
Thanks for sharing!
In theory, it seems possible to have future value span lots of orders of magnitude while not being binary. For example, one could have a lognormal/loguniform distribution with median close to 10^15, and 95th percentile around 10^42. Even if one thinks there is a hard upper bound, there is the possibility of selecting a truncated lognormal/loguniform (I guess not in Metaculus).